Coeficiente de determinação
O coeficiente de determinação ($R^2$) expressa a proporção da variação de uma medida (variável resposta) que é explicada pela variação de outra (variável explanatória). Se supomos que a variação é explicada por uma relação linear, os cálculos são simples e ajudam muito a entender a lógica da partição da variação que está por trás do $R^2$.
Neste roteiro vamos usar a regressão linear e um conjunto pequeno de dados para entender o coeficiente de determinação.
Preparação para o exercício
Para começar, crie uma pasta para você na área de trabalho (desktop) do seu computador. Copie para essa pasta o arquivo com os dados que vamos usar:
Em seguida, abra o programa R, clicando no ícone ![]() que está na área de trabalho do seu computador.
que está na área de trabalho do seu computador.
Se tudo deu certo até aqui, abrirá uma janela do R como essa:
Já com a janela do programa R aberto, o próximo passo será mudar o diretório de trabalho para aquela pasta que você acabou de criar. Com isso será mais fácil importar os dados dos arquivos “.csv” para dentro do ambiente R.
A mudança de diretório deve ser feita da seguinte forma:
- Abra o Menu “Arquivo” (ou “File”);
- Selecione “Mudar dir” (ou “Change dir”);
- Escolha a sua pasta na janela que abrir.
[Obs. Para Mac, essa opção está no Menu “Misc” e a opção é “Change working dir”]
Para checar se você está na pasta correta, copie e cole o comando abaixo na linha de comando do R. Atenção: O comando deve ser colado na frente do símbolo “>”, circundado em azul na imagem anterior. Este símbolo indica o início da linha de comando ou “prompt”, onde você deve escrever comandos para o R.
getwd()
Após colar, aperte a tecla “enter” e veja se o R retorna o nome da sua pasta. Se sim, ótimo. Se não, chame um monitor ou professor.
Importando os dados para o R
Agora vamos importar para o R os dados que você gravou em seu diretório. Para isso copie o comando abaixo, cole na linha de comando do R e pressione “enter”:
dadinhos <- read.csv("dadinho.csv")
Se não houve nenhuma mensagem de erro agora você tem no R uma tabela com 8 linhas e duas colunas, que explicaremos a seguir. Se quiser verificar se a tabela foi importada, digite o nome dela no R
dadinhos
Cálculos passo a passo
A variação total
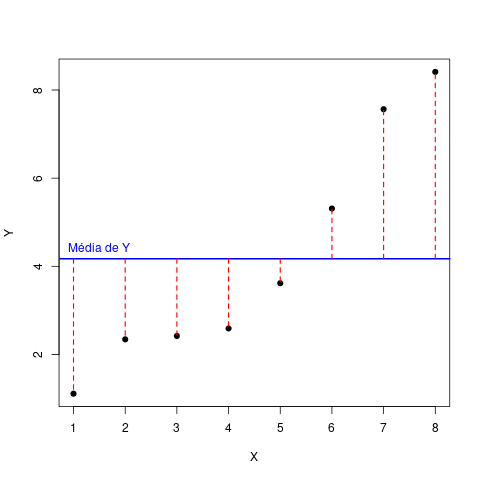
Nosso ponto de partida é a variação de uma variável, no caso Y. Uma das maneiras mais usadas na estatística para expressar a variação de medidas é sua dispersão em torno da média. Para isso, calculamos a diferença de cada medida à média de todas as medidas. Vamos adicionar uma coluna com essas diferenças à nossa tabela de dados:
dadinhos$dif <- dadinhos$Y - mean(dadinhos$Y) dadinhos
Visualmente o que fizemos foi calcular a distância de cada ponto à média de todos os pontos (essas distâncias estão representadas pelos tracejados vermelhos na figura). A média está representada pela linha horizontal azul:
Para resumir essas distâncias em um único número, as elevamos ao quadrado e somamos. Isso é chamado “soma dos desvios quadrados” ou simplesmente “soma dos quadrados”1). Ela expressa a variação total da variável Y.
Calcule essa soma no R com o comando a seguir, e guarde em um objeto chamado V.total
V.total <- sum(dadinhos$dif^2)
Lembrando que, para ver o valor que vc obteve e armazenou nesse objeto, basta digitar o nome do objeto na linha de comando:
V.total
A variação que sobra de uma regressão
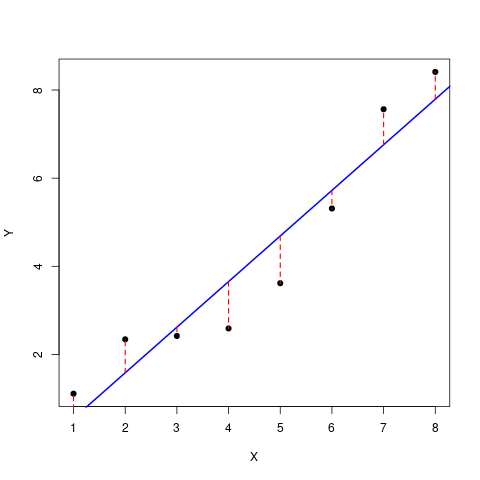
Uma regressão linear busca explicar a variação observada em uma variável (resposta) pela variação de outra (explanatória). Se a regressão é bem sucedida, esperamos que reste bem menos variação sem explicação, que chamamos de variação residual da regressão. Essa variação residual é a “soma dos quadrados dos desvios” de cada ponto à linha de regressão.
Na figura a seguir está a linha da regressão linear de Y em função de X (representada pela linha azul na figura abaixo), e os desvios de cada observação em relação a esta reta de regressão (tracejados vermelhos). Você percebe pela figura abaixo que os desvios (resíduos) da regressão são bem menores que os desvios em relação à média, da figura anterior?
Como chegamos a estes valores na figura? Vamos calcular passo a passo. Primeiro ajustamos a regressão:
dadinhos.lm <- lm(Y ~ X, data=dadinhos)
Os intercepto e a inclinação da equação da reta ajustada são:
(dadinhos.cf <- coef(dadinhos.lm))
E agora adicionamos os valores de Y previstos pela equação da reta para cada valor de X:
dadinhos$Y.pred <- predict(dadinhos.lm)
e também a diferença entre os valores de Y e os previstos, que são os resíduos da regressão:
dadinhos$residuo <- dadinhos$Y - dadinhos$Y.pred
Nossa tabela de dados agora tem cinco colunas:
> dadinhos X Y dif Y.pred residuo 1 1 1.110051 -3.0608617 0.5497765 0.5602747 2 2 2.343195 -1.8277177 1.5843869 0.7588084 3 3 2.420523 -1.7503898 2.6189973 -0.1984742 4 4 2.590459 -1.5804543 3.6536077 -1.0631491 5 5 3.617083 -0.5538302 4.6882181 -1.0711354 6 6 5.311097 1.1401837 5.7228285 -0.4117319 7 7 7.564503 3.3935902 6.7574390 0.8070641 8 8 8.410393 4.2394798 7.7920494 0.6183433
A soma dos quadrados dos resíduos expressa a variação que restou da regressão. É a variação de Y que não é explicada pela variação de X, em uma regressão linear. Para calculá-la somamos os valores da coluna dos resíduos, elevados ao quadrado:
V.resid <- sum(dadinhos$residuo^2)
E vemos que de fato esta variação residual é bem menor que a total (que está no objeto “V.total”):
V.resid
A variação explicada pela regressão
Acima calculamos a variação total de Y e a variação que resta em Y depois de considerarmos um efeito linear de X sobre Y. A soma dos quadrados, medida que escolhemos para expressar estes componentes de variação, tem uma propriedade muito útil. Se consideramos o efeito linear de X como a única fonte de explicação para Y, podemos então dizer que:
$$V_{total} = V_{explic} + V_{resid} $$
ou seja, que a soma dos quadrados total (variação total) é o resultado da adição da soma dos quadrados explicados (pela regressão) e da soma dos quadrados dos resíduos da regressão. Em outras palavras, estamos repartindo, ou particionando aditivamente a variação total de Y em dois componentes2).
Como já calculamos $V_{total}$ e $V_{resid}$ obtemos a variação explicada pela regressão com:
$$V_{explic} = V_{total} - V_{resid} $$
Que podemos calcular no R usando os valores acima, que armazenamos:
(V.expl <- V.total - V.resid)
E finalmente o coeficiente de determinação!
Obtemos o coeficiente de determinação dividindo $V_{explic}$ por $V_{total}$:
V.expl/V.total
Esse coeficiente de determinação é o famoso $R^2$ das regressões lineares!
Neste caso dizemos que 91% da variação de Y é explicada por X. Nada mal. Mas o que você poderia esperar de dados que a gente mesmo criou, né?