Índice
Roteiros
- Populações
-
- Estrutura
-
- Dinâmica
-
- Denso Independente
-
- Denso Dependente
-
- Populações Estruturadas
-
- Metapopulações
-
- Uma Espécie
-
- Duas Espécies
-
- Comunidades
-
- Estrutura
-
- Dinâmica e Distúrbio
-
- Dinâmicas Neutras
-
- Matemática e Estatística
-
- Cálculo Integral e Diferencial
-
- Processos Estocásticos
-
Links Externos
Visitantes




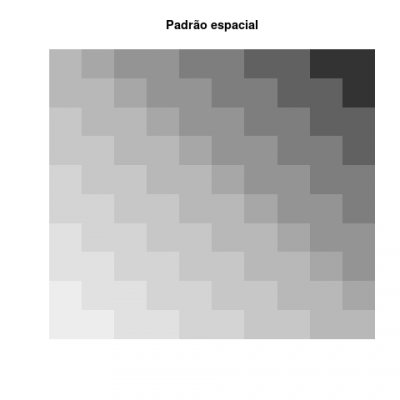
 A parcela no vértice inferior à esquerda é a parcela número 1 da planilha e a parcela no vértice superior à direita é a parcela numero 100 da planilha. Dê uma conferida rápida se os valores de abundância das 10 espécies nessas duas parcelas (1 e 100) faz sentido com o que está sendo visualizado nos mapas acima.
A parcela no vértice inferior à esquerda é a parcela número 1 da planilha e a parcela no vértice superior à direita é a parcela numero 100 da planilha. Dê uma conferida rápida se os valores de abundância das 10 espécies nessas duas parcelas (1 e 100) faz sentido com o que está sendo visualizado nos mapas acima.