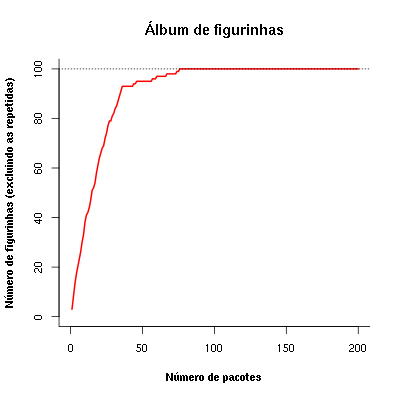
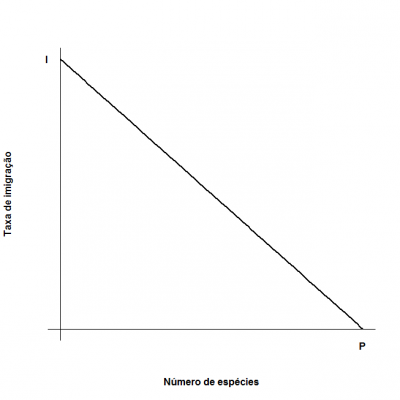
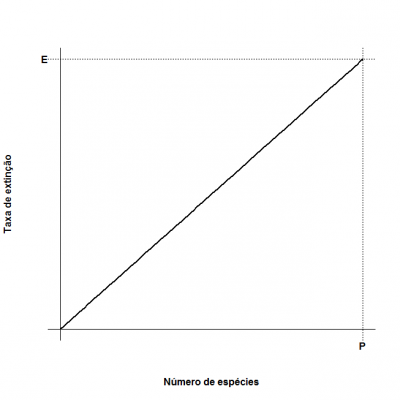
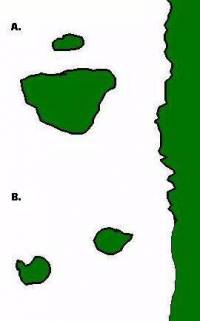
Contents
Tutorials
- Population
-
- Structure
-
- Dynamics
-
- Density-independent
-
- Density-dependent
-
- Strutured Population
-
- Metapopulation
-
- Single Species
-
- Two Species
-
- Community
-
- Estrutura
-
- Dynamics and Disturbances
-
- Dinâmicas Neutras
-
- Mathematics & Statistics
-
- Differential and Integral Calculus
-
- Stochastic Processes
-
Links Externos
Visitors