−Table of Contents
ATENÇÃO: ESTA PÁGINA É UMA VERSÃO ANTIGA DO ROTEIRO E ESTÁ DESATIVADA, PARA ACESSAR O ROTEIRO ATUAL ACESSE ESTE LINK
Metapopulações com colonização interna - Roteiro no EcoVirtual
No modelo de Metapopulations and propagule rain - Tutorial in EcoVirtual a colonização era constante e independente da fração de manchas ocupadas. Eliminando o pressuposto de uma chuva de propágulos constante e relacionando a colonização com a fração de manchas ocupados chegamos ao modelo clássico de metapopulações descrito por Richard Levins em 1969. Em uma formulação simples desse modelo, a fonte de propágulos é unicamente interna (sistema fechado) e a probabilidade de colonização varia de forma linear à proporção de lugares ocupados.
Modelo matemático
Nessa formulação, nosso modelo não terá mais uma probabilidade de colonização constante (pi), mas sim uma probabilidade de colonização dependente do número de manchas ocupadas:
pi=if
onde i é uma constante que indica quanto aumenta a probabilidade de colonização a cada nova mancha que é ocupada. Portanto, quanto mais manchas ocupadas, maior a chance de colonização das manchas vazias. Substituindo pi na equação antiga temos:
dfdt=if(1−f)−pef
Equilíbrio
O cálculo da fração de manchas ocupadas no equilíbrio (ˆf→dfdt=0) também é modificado para:
ˆf=1−pei
Simulação
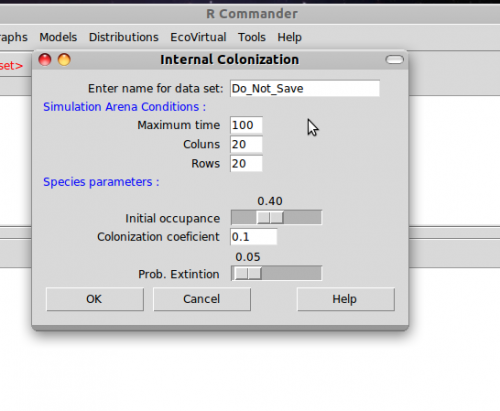
Vamos tentar entender esse modelo a partir da simulando computacional desse cenário. Como no roteiro Metapopulations and propagule rain - Tutorial in EcoVirtual, criamos uma função no R para gerar a simulação. Esta função sorteia eventos de colonização e extinção em cada mancha a cada intervalo de tempo, segundo as regras do modelo e os parâmetros definidos pelo usuário. Em seguida retorna um gráfico da trajetória do número de manchas ocupadas e as matrizes de ocupação das manchas em cada instante de tempo. Para rodar esse modelo no EcoVirtual entre os valores dos argumentos na janela da opção de Internal colonization do sub-menu Metapopulation
Nesse menu os argumentos são:
| opção | parâmetro | definição |
|---|---|---|
| data set | objeto no R | guarda os resultados |
| Maximum time | tmax | Número de iterações da simulação |
| columns | ncol | número de colunas de habitat da paisagem |
| rows | nrows | número de linhas de habitat da paisagem |
| initial occupance | f0 | no. de manchas ocupadas no inicio |
| colonization coef. | i | coeficiente de colonização i |
| prob. extinction | pe | probabilidade de extinção |
E agora você pode simular o modelo com os valores que escolher para os argumentos da função, como:
tmax=100;ncol=10;nrow=10;f0=0.1;i=1;pe=0.5
Brinque um pouco com o modelo variando os parâmetros e tentando responder as seguintes perguntas:
- Você consegue perceber alguma diferença nos resultados dos dois modelos (seed rain e internal colonization), mantidos iguais os parâmetros que eles têm em comum?
- A posição de uma mancha na paisagem influencia a pi e a pe dessa mancha? Qual seria um modelo mais realista?
- Por que há certas combinações de i e pe que não podem existir1)?
- Qual o significado de um ˆf negativo?
- Em qual situação o equilíbrio é ˆf=1?
Sugestões de cenários
- tmax=100;
- ncol=10;
- nrow =10;
- f_0=0.1;
- i=0.5;
- pe=0.5
Para saber mais
- Gotelli, N. 2007. Ecologia. Londrina, Ed. Planta. Capítulo 4.
- Stevens, M. H. 2009. A primer of ecology with R. New York. Springer.Capítulo 4.
- Gotelli, N. 1991. Metapopulation models: the rescue effect, the propagule rain, and the core-satellite hypothesis. The American Naturalist, 138: 768-776. pdf no site do autor
Código R
- Entre aqui para seguir o roteiro utilizando diretamente o código do R