−Table of Contents
Metapopulations and propagule rain - Tutorial in EcoVirtual
Equilibrium
Using EcoVirtual
To proceed, you must have the R environment with the Rcmdr and Ecovirtual packages installed and loaded. If you do not have and do not know how to have them, see the Installation page.
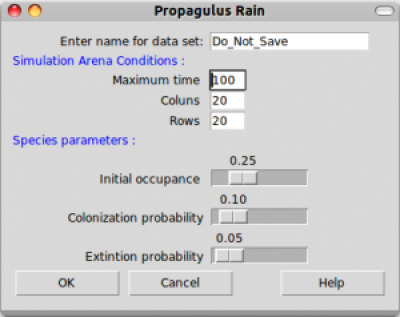
Caso tenha seguido as instruções da página de instalação, partindo da premissa que as instruções funcionam, terá na tela a janela do Rcmdr aberta e uma opção de menu EcoVirtual. Clique nesse menu e depois em Metapopulation em seguida em Seed Rain…. A seguinte janela de opções deve se abrir: