Dinâmica populacional denso-independente - Roteiro no Ecovirtual

Uma população em que as taxas de nascimento e mortalidade são constantes tem um crescimento ou decréscimo independente da densidade dela própria. Essa situação é geralmente relacionada à ausência de restrição ao crescimento, quando os recursos são ilimitados, mas pode também estar associada à extinção de populações.

Vamos imaginar agora uma população com taxas constante de crescimento e mortalidade e sem migrações. A população cresce ou é observada a intervalos regulares. O tamanho da população no próximo passo de tempo ($N_{t+1}$) é o número de indivíduos da geração anterior ($N_t$) mais o número de nascimentos (B), e menos o número mortes (D) no intervalo de tempo:

$$N_{t+1} = N_t + B - D $$

O número de mortes e nascimentos são resultado de taxas per capita multiplicadas pelo tamanho da população:

• $ B=bN_t $
• $ D=dN_t $

onde: $b$ = taxa de nascimento per capita a cada geração ; $d$ = taxa de mortalidade per capita a cada geração. Note que a taxa não muda com o tamanho da população, e que o número de nascimentos e mortes é proporcional ao tamanho populacional. Vamos apenas deixar claro mais uma premissa, para fins didáticos: os nascimentos e mortes ocorrem simultaneamente na população, no intervalo de tempo $t$. Podemos então dizer que :

• $N_{t+1} = N_t + bN_t-dN_t $
• $N_{t+1} = N_t + (b-d)N_t $

se definimos um fator de crescimento discreto: $r_d = b-d$

• $N_{t+1} = (1+r_d)N_t$
• $\frac{N_{t+1}}{N_t} = 1+r_d$

Como $ 1+r_d $ é uma constante, vamos designá-la como $\lambda$, um número positivo que expressa o aumento proporcional da população de uma geração a outra. Portanto:

$$ \lambda=\frac{N_{t+1}}{N_t} \implies N_{t+1} = \lambda N_t$$

Podemos então projetar a nossa população a cada passo de tempo $t$. Por exemplo:

Se uma população com 100 indivíduos tem uma taxa per capita de natalidade de 0,8/ano e de mortalidade de 0,75/ano, qual o tamanho esperado da população no próximo ano?

$$N_{t+1}=100 \times (1+0,8-0,75) = 100 \times 1,05 = 105$$

Podemos também projetar a população para outras gerações, usando iterações:

• $N_{t+2} = 105 \times 1,05 = 110,25$
• $N_{t+3} = 110,25 \times 1,05 = 115,7625$

prosseguindo e tomando o tamanho da população no tempo zero ($N_0$):

• $N_{t+4}= N_0 \times \lambda \times \lambda \times \lambda \times \lambda$
• $N_{t+4}= N_0 \lambda^4 $

Generalizando:

$$N_{t}=N_0 \lambda^t $$

Assim, para nosso exemplo a projeção para 10 intervalos de tempo é

$$100 \times {1,05}^{10} = 162,8895$$

Com um pouco de manipulação algébrica a equação para tempo discreto

$$N_{t+1} \ = \ (1+r_d)N_t$$

Pode ser reescrita como

$$ N_{t+1} - N_t \ = \ \Delta N \ = \ r_dN_t $$

o que explicita que a velocidade de crescimento $\Delta N = N_{t+1} - N_t$ é proporcional ao tamanho poulacional $N_t$. Essa é característica essencial do crescimento populacional sem limites a uma taxa constante:

A velocidade de crescimento é a variação no número de indivíduos $\Delta N$ dividida pelo tempo em que se deu esta variação, $\Delta t$. No modelo de tempo discreto $\Delta t = 1$, por definição. É um intervalo que pode ser tão grande como uma geração. Isso faz sentido se as mudanças no tamanho populacional se dão em intervalos discretos, como por exemplo em espécies semélparas com estação reprodutiva sincronizada.

No entanto, o tamanho populacionais da maioria das espécies varia continuamente. O cálculo diferencial foi criado para descrever esse tipo de dinâmica. Como o problema é que podem ocorrer mudanças a qualquer instante, o conceito-chave aqui é o de taxa instantânea, ou derivada.

Se nascimentos e mortes podem acontecer a todo momento, faz mais sentido pensarmos em uma velocidade instantânea do tamanho populacional. Isto equivale a reduzir $\Delta t$ tanto que pode ser considerado um instante. Esta velocidade instantânea é a derivada do tamanho populacional, que representamos com ${dN}/{dt}$, para diferenciar da velocidade a intervalos grandes e arbitrários $\Delta N/\Delta t$ ²⁾.

Agora podemos expressar que velocidade instantânea de uma população é proporcional ao tamanho populacional com a equação:

$$\frac{dN}{dt} = rN$$

Que é o modelo de crescimento populacional a taxa constante em tempo contínuo. O parâmetro $r$ é chamado taxa instântanea de crescimento per capita. Essa taxa $r$ expressa o número médio de filhotes que cada indivíduo da população produz num intervalo de tempo muito curto. Por isso, muito livros de ecologia indicam que a unidade de $r$ é indivíduos/indivíduo.tempo. Físicos e matemáticos são mais rigorosos e lembram que a expressão correta da unidade é 1/tempo.

Para prever o tamanho de uma população que cresce a uma taxa constante em tempo contínuo usamos a equação

$$N(t) = N_0e^{rt}$$

E a relação entre a taxa de crescimento instantânea e a taxa de crescimento do modelo discreto é

$$ r \ = \ ln(\lambda)$$

Vamos usar o EcoVirtual para projetar o tamanho de populações que crescem a taxas constantes sem limite, em tempo contínuo e discreto.

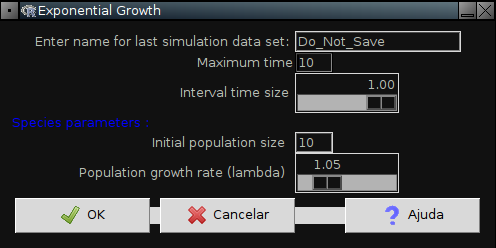
Na janela do Rcmdr clique na opção de menu EcoVirtual, e depois em One population em seguida em Exponential growth. Duas janelas irão se abrir, uma de opções como esta

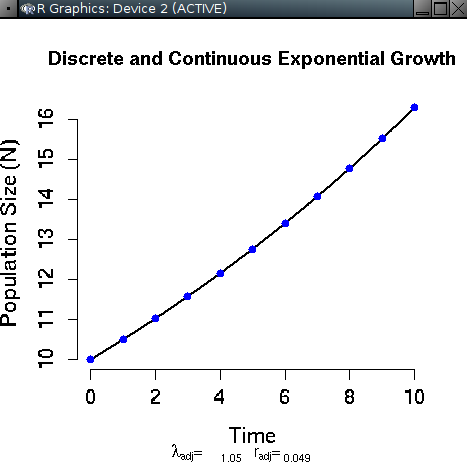
e outra com um gráfico como este:

Arranje as janelas de modo que o gráfico esteja sempre visível, mesmo quando você alterar valores na janela de opções.

Ele mostra o tamanho da população em função do tempo previstos pelos modelos. Os pontos azuis indicam os tamanhos populacionais previstos pelo modelo de crescimento em tempo discreto

$$N_t = N_0\lambda^t$$

usando os valores de $N_0$ e $\lambda$ da caixa de opções. A linha preta indica os tamanhos populacionais previstos pelo modelo de crescimento em tempo contínuo

$$N(t) = N_0e^{rt}$$

usando os mesmos valores da caixa de opções. Para isso, o $\lambda$ da caixa de opções é usado para calcular a taxa de crescimento instantânea per capita correspondente do modelo contínuo pela relação:

$$r=ln(\lambda)$$

Os valores para o modelo discreto são pontos, porque este modelo prevê o tamanho da população a intervalos discretos. Já o modelo em tempo contínuo prevê o tamanho da população a qualquer momento, e por isso é representado por uma linha contínua.

Os pontos se sobrepõem à linha porque o EcoVirtual usa taxas de crescimento equivalentes para tornar as projeções comparáveis. Abaixo do eixo X do gráfico está o valor de $\lambda$ e de $r$ usados na simulação.

Nesta janela você pode alterar os parâmetros da projeção, o que atualiza o gráfico:

Em suas memoráveis aulas de dinâmica de populações, o físico Roberto Kraenkel costuma dizer que não sabe se o paraíso existe, mas em caso afirmativo sabe que só lá as populações crescem sem limites. Apesar disso, prossegue, os modelos para este tipo de crescimento são essenciais para entender a dinâmica de populações reais, assim como a irrealista primeira lei de Newton é essencial para entender o movimento dos corpos no espaço.

Então vamos usar o EcoVirtual para explorar o comportamento dos modelos de crescimento a taxas constantes!

Experimente diferentes valores da taxa de crescimento discreto $\lambda$ com a opção Population growth rate (lambda) da janela de opções. Isso vai alterar também a taxa de crescimento contínuo $r$. Veja o efeito no gráfico e use uma calculadora para conferir a correspondência entre as duas taxas, indicadas abaixo do eixo X do gráfico.

Qual valor ou intervalos de valores de $\lambda$ e de $r$ sob o quais a população:

1. cresce ?
2. descresce ?
3. permanece estável ?

A opção Interval time size define um novo intervalo de tempo para o modelo de tempo discreto. O novo valor de intervalo é uma fração do original de valor um. Assim, se você escolher $0.5$ para esta opção as projeções do modelo discreto são recalculadas para intervalos que correspondem à metade do intervalo original. Por isso, você verá no gráfico pontos azuis a cada meia unidade de tempo. Alterando o intervalo para $0.25$ você terá projeções para intervalos que são um quarto da unidade original, e o gráfico terá pontos a cada 0,25 unidade de tempo.

Note que à medida que você diminui o intervalo de tempo do modelo discreto os pontos se aproximam, até que parecem formar uma linha contínua. Ou seja, a projeção a intervalos discretos tende à projeção em tempo contínuo à medida que os intervalos são reduzidos!

De fato, o modelo exponencial pode ser visto como um limite do modelo discreto. Os detalhes estão no já indicado roteiro taxas, derivadas e função exponencial. Mas para que isso funcione o EcoVirtual recalcula o valor de $\lambda$ e o correspondente $r$ para cada novo intervalo de tempo discreto. E aqui vai nossa pergunta: como são feitos estes cálculos? Mais precisamente:

Dado uma razão de crescimento discreto para um intervalo de tempo de valor de uma unidade, $$\lambda_1=\frac{N_{t+1}}{N_t}$$

como calcular a razão de crescimento para um intervalo fracionário

$$\lambda_{1/n}=\frac{N_{t+{1/n}}}{N_t}$$

de modo que ao final de uma unidade de tempo a razão de crescimento permaneça $\lambda_1$? Verifique sua solução contra os valores que o EcoVirtual retorna quando você reduz o intervalo de tempo discreto pela metade (opção Interval time size=0.5).

• Gotelli, N. J. 2007. Ecologia. Planta, Londrina. O capítulo 1 é uma introdução muito didática aos modelos de crescimento sem dependência da densidade.
• Population dynamics from first principles. Capítulo 2 de Complex Population Dynamics. Peter Turchin, Princeton Univ Press, 2003. Este texto instigante defende que o modelo de crescimento exponencial está para a biologia como as leis de Newton estão para a física.
• Vandermeer, J. 2010. How Populations Grow: The Exponential and Logistic Equations Nature Education Knowledge 3(10):15. Outro texto muito didático, com considerações sobre as consequências ambientais do crescimento populacional humano.