−Tabela de conteúdos
Coexistência em Metapopulações - Roteiro no EcoVirtual
Sob quais condições as espécies podem coexistir? Há várias hipóteses, mas neste exercício vamos investigar o papel do regime de perturbação que uma área sofre, e das diferenças na capacidade de colonização das espécies. Estamos ainda enfatizando os processos de colonização e extinção, decritos pelos modelos de metapopulações.
Vamos partir do modelo metapopulações com colonização interna, que tem uma espécie cuja dinâmica da proporção de manchas já é bem conhecida de vocês:
df1dt=i1f1(1−f1)−pef1
onde:
- f1 = fração de machas ocupadas pela espécie 1
- pe = probabilidade de extinção por mancha
- ii = taxa de incremento da probabilidade de colonização da espécie 1 com o aumento de f
- A taxa de colonização, portanto, é o produto i1f1, e varia com a fração de manchas ocupadas (quanto mais ocupação, mais propágulos).
Agora vamos acrescentar mais uma espécie ao sistema 1). Esta espécie será uma competidora fraca: só permanece em manchas desocupadas. Isto significa que as manchas disponíveis para sua colonização são apenas as vazias, e que ela é excluída se uma mancha que ocupa é colonizada pela outra espécie. A variação da fração de manchas ocupadas por esta espécie é definida como:
df2dt=i2f2(1−f1−f2)−i1f1f2−pef2
Fatos importantes sobre o modelo
Interpretação
A equação para a espécie 2 não tem nenhum coeficiente novo, apenas combinações diferentes deles:
- O termo i2f2(1−f1−f2) indica que a fração de manchas colonizadas é proporcional à fração de manchas vazias, ou seja, sem nenhuma das duas espécies.
- O termo i1f1f2 é a fração esperada de manchas ocupadas pela espécie 2 que são colonizadas pela espécie 1. Portanto, é a fração de manchas das quais a espécie 2 é excluída pela chegada da espécie 1.
- A taxa de extinção é igual à da espécie 1, por isso não tem subscrito.
Equilíbrio
A fração de manchas ocupadas pela espécie 1 no equilíbrio permanece:
ˆf1=1−pei1
E a fração de manchas ocupadas pela espécie 2 no equilíbrio é:
ˆf2=pei1−i1i2
Portanto, para que a metapopulação da espécie 2 seja viável neste modelo (ˆf2>0), é preciso satisfazer a desigualdade
pei1>i1i2
De onde veio isto?
A dedução dos valores em equilíbrio pede apenas manipulações algébricas muito simples. Se você ainda se assusta com matemática, tenha em mente que o essencial é compreender a lógica de cada passo de dedução. Para as manipulações em si, há programas de matemática simbólica que podem lhe ajudar, como o MAXIMA, que é de uso livre 2).
Caso queira conhecer essa instrumentação, baixe e instale o programa com sua interface gráfica wxMaxima, em seguida abra esse arquivo aqui com os comandos e tecle crtl-R para executar cada linha de comando.
Simulação
Para prosseguir você deve ter o ambiente R com os pacotes Rcmdr e Ecovirtual instalados e carregados. Se você não tem e não sabe como ter, consulte a página de Instalação.
Caso já tenha o R e pacotes instalados
Carregue o pacote principal RcmdrPlugin.EcoVirtual pelo menu do R Pacotes > Carregar Pacotes, ou pela linha de comando com o código:
library("RcmdrPlugin.EcoVirtual")
Vamos usar simulação computacional para gerar uma dinâmica estocástica que segue as regras do modelo de equações diferenciais da variação na proporção de manchas ocupadas para as duas espécies, descritas acima. A simulação é bastante parecida com as usadas nos exercícios de metapopulações. A seguir descrevemos a sequência de instruções que o EcoVirtual executa 3). Leia com atenção e imagine o programa processando as informações como se fosse um tabuleiro em que cada casa pode ter três estados: vazio, ocupada com a espécie 1 ou ocupada com a espécie 2.
Pseudocódigo
- Defina uma matriz com linhas (rw) e colunas (cl). Cada célula da matriz é uma mancha.
- Defina as frações de manchas ocupadas pelas duas espécies (f01 e f02) e ocupe as manchas ao acaso com estas proporções.
- Calcula as probabilidades de colonização das duas espécies, que é o produto pi=i×f.
- Entre as manchas ocupadas, sorteie as que serão desocupadas, usando a probabilidade de extinção (pe).
- Entre as manchas não ocupadas pela espécies 1, sorteie as que serão ocupadas por ela, de acordo com a probabilidade de colonização (i1×f1).
- Entre as manchas desocupadas, sorteie as que serão ocupadas pela espécie 2, de acordo com a probabilidade de colonização. Nas manchas colonizadas pela espécie 1 (item anterior), a colonização pela espécie 2 não tem sucesso.
- Conte o número de manchas ocupadas por cada espécie e divida pelo total de manchas para obter as frações ocupadas.
- Reitere a partir do passo 3 até o número de intervalos desejado.
Competição de Metapopulações no Ecovirtual
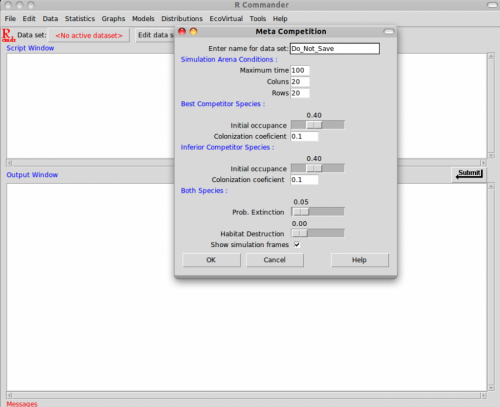
Para o roteiro das simulações aqui sugeridas é necessário apenas abrir a Meta Competition que se encontra no menu EcoVirtual>Two species> Meta Competition… . A janela dos parâmetros do modelo se abrira:
Os parâmetros aqui são os mesmos da colonização interna, com a adição de uma nova espécie:
| opção | parâmetro | definição |
|---|---|---|
| data set | objeto no R | guarda os resultados |
| Maximum time | tmax | Número de iterações da simulação |
| columns | cl | número de colunas de habitat da paisagem |
| rows | rw | número de linhas de habitat da paisagem |
| Best Competitor | Parâmetros para a melhor competidora | |
| initial occupancy | f01 | proporção de manchas ocupadas no inicio pela sp1 |
| colonization coef. | i1 | coeficiente de colonização i das sp1 |
| Inferior Competitor | Parâmetros para a pior competidora | |
| initial occupancy | f02 | proporção de manchas ocupadas no inicio pela sp2 |
| colonization coef. | i2 | coeficiente de colonização i da sp2 |
| Both Species | Parâmetros comuns para as duas espécies | |
| prob. extinction | pe | probabilidade de extinção |
| Habitat Destruction | D | proporção de manchas não disponibilizadas |
| Show simulation frames | anima=TRUE | mostra cada tempo simulado |
Qual o segredo da coexistência?
Comece com uma simulação com estes parâmetros:
tmax = 100 cl = 20 rw = 20, f01 = 0.1 f02 = 0.4 i1 = 0.4 i2 = 0.5 pe = 0.25
Calcule o valor de equilíbrio para cada espécie segundo as fórmulas do tópico acima Equilibrio. Verifique se os valores teóricos (calculados) de F1 e F2 são coerentes com o valor da simulação.
Balanço Competição x Colonização
Não seja destrutivo!
O parâmetro D no modelo controla a quantidade de habitat destruído no início da simulação. Não vamos, ainda, mostrar nossa imensa capacidade destrutiva, isso faz parte do próximo roteiro. Por enquanto deixe o parâmetro sempre em zero.
Definimos a espécie 2 como uma pior competidora. Isto a condena sempre à extinção? Estude o efeito de diferenças nas habilidades de colonização sobre a coexistência. Para isto, faça variar o parâmetro de colonização da espécie 2, mantendo os demais constantes. Identifique as condições de coexistência, e de extinção de cada espécie.
Inicie com os seguintes parâmetros:
tmax = 100 cl = 20 rw = 20 f01 = 0.05 f02 = 0.05 i1 = 0.1 i2 = 0.1 pe = 0.05
Agora mantenha tudo constante e mude apenas o parâmetro i2 para:
- de 0.2 até 1 a cada 0.1
- 10
- 100
Interprete os resultados.
A condição para persistência da espécie 2 é uma desigualdade que envolve a razão i1/i2, que expressa as diferenças nas habilidades de colonização das duas espécies. Veja as fórmulas no tópico Equilibrio
Regime de Extinção
Vamos começar a simulação com uma nova combinação de parâmetros, em que espécie 2 tem o triplo de capacidade de colonização que a espécie 1:
tmax = 100, cl = 20, rw = 20, f01 = 0.1, f02 = 0.1, i1 = 0.1, i2 = 0.3, pe = 0.05
Há extinção regional (todas as manchas) de alguma espécie nessa simulação? Faça variar a probabilidade de extinção mantendo os demais parâmetros constantes, para investigar o efeito do regime de perturbação sobre este resultado:
- aumente o pe para 0.07
- varie o pe de 0.08 a 0.14 a cada 0.02
Caso não chegue ao equilíbrio:
Dicas
Muitas vezes para conferir se realmente o sistema tende ao equilíbrio teórico é necessário aumentar o tempo da simulação. Quando a animação está ativada, isso pode demorar um pouco para ser processado. Para evitar demoras, desligue a animação tirando a seleção do “Show simulation frames” (anima=FALSE).
Proporção de manchas ocupadas inicial
Ocupância pode ser definida como a proporção de manchas disponíveis ocupadas pela espécie. No nosso modelo a ocupância inicial das espécies é definida pelos parâmetros f01 e f02
- produza simulações para verificar se esses parâmetros alteram o destino das populações
- as trajetórias das simulações varia com valores de ocupância diferentes? E a coexistência a longo prazo?
Perguntas
- Que atributos da espécie competitivamente inferior propiciam coexistência com a espécie competitivamente superior? Interprete em termos biológicos e apresente as simulações para embasar sua argumentação.
- Qual a relação entre coexistência e a extinção em manchas neste modelo? Pense em consequências teóricas e aplicadas.
- Qual o efeito da espécie 2 sobre a espécie 1 neste modelo? Demonstre isso de forma bastante clara em uma simulação.
- Qual o valor de equilíbrio da espécie 2 quando a espécie 1 não está presente?
Referências
- Hastings, A. (1980) Disturbance, coexistence, history and competition for space. Theoretical Population Biology, 18:363–373.
- Stevens, M.H.H. (2009) A primer in ecology with R. New York, Springer.