Índice
Roteiros
- Populações
-
- Estrutura
-
- Dinâmica
-
- Denso Independente
-
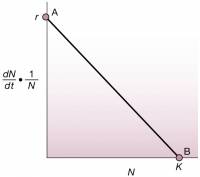
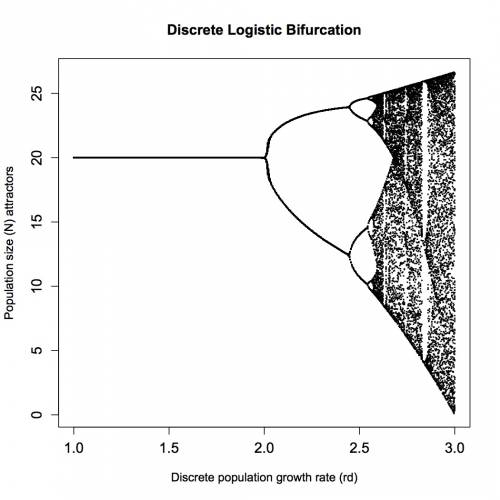
- Denso Dependente
-
- Populações Estruturadas
-
- Metapopulações
-
- Uma Espécie
-
- Duas Espécies
-
- Comunidades
-
- Estrutura
-
- Dinâmica e Distúrbio
-
- Dinâmicas Neutras
-
- Matemática e Estatística
-
- Cálculo Integral e Diferencial
-
- Processos Estocásticos
-
Links Externos
Visitantes





![[[http://en.wikipedia.org/wiki/Marmot]] [[http://en.wikipedia.org/wiki/Marmot]]](/lib/exe/fetch.php?w=150&tok=0e45fb&media=http%3A%2F%2Fupload.wikimedia.org%2Fwikipedia%2Fcommons%2Fthumb%2F3%2F3b%2FMarmot-edit1.jpg%2F320px-Marmot-edit1.jpg)