−Tabela de conteúdos
Sucessão
Um dos objetivos da Ecologia é entender como ocorre a Sucessão, ou seja, as mudanças na estrutura de comunidades ao longo do tempo. Esse processo inicia-se quando um local desocupado, seja por falta de condições adequadas ou algum distúrbio que removeu a comunidade anterior, passa a ser colonizado. Em geral, o início da colonização é feito por espécies pioneiras, que possuem alta fecundidade e potencial de dispersão, com altas taxas de crescimento. Por outro lado, como já sabemos 1), essa espécie provavelmente será substituída por outra, melhor competidora.
Uma observação recorrente é que, após certo tempo, a comunidade se estabiliza, o que gerou alguns modelos teóricos sobre a sucessão:
- Modelo de Facilitação: as espécies pioneiras, únicas que podem sobreviver no ambiente hostil, alteram o mesmo, dando condições para espécies secundárias, que as eliminam. O mesmo acontece com as novas espécies, até que se atinge o clímax: a comunidade é formada por um grupo de espécies resistentes a invasões e só é destruída por distúrbio.
- Modelo de Inibição: ao contrário do anterior, este prega que as espécies colonizadoras são boas competidoras e reprimem a chegada de novas espécies.
- Modelo de Tolerância: este é um modelo que segua a Teoria Neutra, onde as interações bióticas e fatores ambientais não influenciam na sucessão.
Modelos Matriciais de Sucessão
A álgebra matricial pode ser usada para modelar essas transições de fases em um conjunto de manchas, como fizemos na aula de modelos matriciais de Leslie e Leftkowitch. Por trás desses modelos estão as cadeias de Markov 2), que utilizaremos também no modelo Neutro de Hubbell.
A ideia aqui é a mesma do modelo matricial de populações: uma matriz de transição (A) representando as probabilidades de transição de cada estado de um tempo a outro, multiplicada pelo vetor de número de manchas em cada estado (s(t)) nos dá o número do estado no intervalo de tempo seguinte:
s(t+1)=A∗s(t)
Onde:
Matrizes de Transição
Conforme dito acima, matrizes de transição são matrizes quadradas, onde as colunas representam os estados atuais enquanto as linhas representam os próximos estados. As entradas são as probabilidades 6) de transição do estado atual (coluna) para o próximo (linha).
Para cada estado atual, todas as possibilidades devem estar representadas. Por isso a soma das colunas deve totalizar 1.
Vamos entender com um exemplo:
| Estado no tempo t | |||||
|---|---|---|---|---|---|
| Aberto | Herbáceo | Arbustivo | Floresta | ||
| Estado t+1 | Aberto | 0,65 | 0,23 | 0,25 | 0,40 |
| Herbáceo | 0,15 | 0,70 | 0,25 | 0,10 | |
| Arbustivo | 0,00 | 0,07 | 0,25 | 0,15 | |
| Floresta | 0,20 | 0,00 | 0,25 | 0,35 | |
Observando o estado atual Aberto (coluna 1), sabemos que há 65% de chance de ele continuar Aberto, 15% de virar Herbáceo e 20% de virar Floresta. Note que, como a terceira linha desta coluna é 0, não há possibilidade de em espaço Aberto virar Arbustivo no próximo passo e que a soma de todas as probabilidades dá 1.
Outro caso interessante é quando o Arbustivo é o atual: há iguais chances (25%) para que qualquer estado seja o próximo.
A diagonal representa a probabilidade de que a mancha se mantenha no mesmo estado.
As transições também podem ser representadas graficamente:
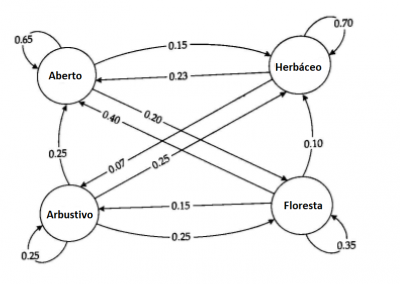
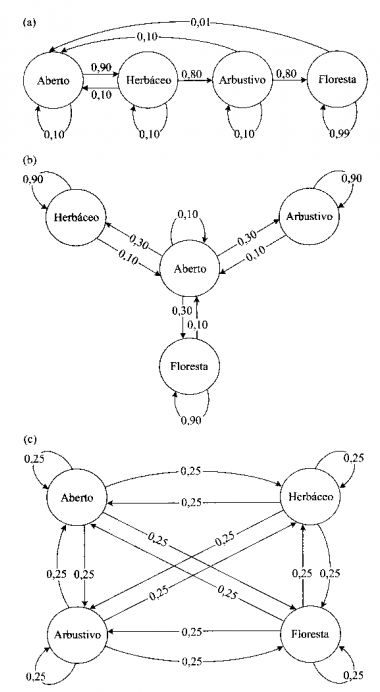
- Monte as matrizes da cada representação gráfica.
- Você consegue associar cada matriz a um dos modelos teóricos vistos na primeira sessão?
ATENÇÃO: Guarde seus resultados, pois serão utilizados posteriormente.
Simulação
Vamos simular esse modelo no Excel, incluindo também distúrbio, representado retorno ao estado Aberto.
- 1. Nas células C4:F7, produza a matriz (A) que usamos como exemplo:
- 2. Nas células I4:I7, produza o vetor de distribuição de estados inicial (s(1)):
| Número de Manchas no início | |
|---|---|
| Aberto | 250 |
| Herbáceo | 100 |
| Arbustivo | 80 |
| Floresta | 70 |
- 3. Agora vamos calcular nas células J4:J7 a distribuição de estados em t=2 (s(2)). Para isso, faça a multiplicação s(2) = A * s(1) de acordo com as seguintes instruções:
- 3.1. Selecione a célula J4, clique no menu INSERIR/FÓRMULA/MATRIZ (Excel) e escolha a função de multiplicação de matrizes, (M.MULT ou MATRIZ.MULT dependendo da versão do programa). Indique, na caixa de diálogo da função, o que deve ser multiplicado: primeiro a matriz de transição (C4: F7) e depois o vetor da população (I4:I7). Clique “OK” para finalizar.
Dica! Para evitar retrabalho e facilitar as próximas simulações, fixe a matriz de transição. Para isso, acrescente $ antes das colunas e índices da matriz na fórmula, conforme figura abaixo:
- 3.2. O resultado dessa multiplicação deveria ser um vetor com 4 linhas. Caso o seu tenha ficado neste padrão, ignore este passo. Caso tenha aparecido apenas um valor, selecione a célula com a fórmula (J4) e as abaixo (J5:J7) 7), pressione F2 (para abrir a fórmula) e em seguida Control + Shift+ Enter. Isso deve resolver!
ATENÇÃO: depois de feito o truque acima, sempre que tentar alterar uma célula da nova matriz criada, o Excel mostrará uma mensagem de erro; para fugir dessa armadilha não adianta ficar apertando ENTER; a saída é o ESC.
- 4. Repita as projeções de população para 20 ciclos de tempo. Caso você tenha fixado a matriz de transição conforme a dica, basta copiar o vetor do tempo 2 e copiá-lo nas próximas 18 colunas. Apenas certifique-se que a fórmula esta sendo copiada com as referências corretas.
- 5. Crie gráficos com as trajetórias dos estados.
- Você consegue observar um padrão nas quantidades de manchas em cada estado conforme o tempo aumenta? Por que ele é causado?
- Experimente duplicar esta aba no Excel e alterar os valores da população inicial (I4:I7), mas mantendo o tamanho total de manchas = 500. Agora compare s(20) das duas simulações.
Tipos de Sucessão
Lembra das matrizes que montamos de acordo com as representações gráficas? Agora podemos simula-las:
- Simule os modelos de sucessão de (a)facilitação, (b) inibição e (c ) tolerância. Você pode usar as matrizes que montamos ou criar novas, desde que não percam a ideia de cada modelo.
- Compare os modelos.
- Aumente o distúrbio no estado de Floresta (transição para Vazio) e veja como o sistema se comporta nos três modelos.
Discuta:
- Qual desses modelos tem maior paralelo com a sucessão em florestas? Por que?
- O aumento do distúrbio pode gerar a exclusão de alguma fase no sistema? Por que?
Vegetação do Deserto
Em seu trabalho no deserto de Sonora (Califórnia - EUA), McAuliffe estudou a dinâmica no deserto para três estados de um alteração sucessional muito lenta. Esses estados são caracterizados pela chaparra (Larrea tridentata), a ambrósia americana (Ambrosia ambrosioides) e por espaços vazios.
 No centro da foto encontra-se a chaparra (Larrea tridentata) um arbusto que pode se tornar uma arvoreta (detalhe da flor) e no canto direito um detalhe da ambrósia americana
No centro da foto encontra-se a chaparra (Larrea tridentata) um arbusto que pode se tornar uma arvoreta (detalhe da flor) e no canto direito um detalhe da ambrósia americana
A matriz de transição construída com dados observados em campo é a seguinte:
| Estado no tempo t | ||||
|---|---|---|---|---|
| Aberto | Ambrosia | Larrea | ||
| Estado t+1 | Aberto | 0,99854 | 0,031 | 0,0016 |
| Ambrosia | 0,0013 | 0,96842 | 0 | |
| Larrea | 0,00016 | 0,00058 | 0,9984 | |
Construa o diagrama desse modelo, como no esquema dos tipos de sucessão, e faça também a simulação no Excel.
- 1. Em qual dos modelos de sucessão acima a dinâmica dessa matriz pode ser classificada?
- 2. É possível identificar algum tipo de facilitação no sistema? Se sim, há como medir essa facilitação?
- 3. Qual a frequência de estado esperado para o equilíbrio nesse sistema 8)?
- 4. Quanto tempo o sistema demoraria a chegar ao estado de equilíbrio, caso algum distúrbio deixasse todas as manchas vazias 9)?
- 5. Há diferenças no estado de equilíbrio se partirmos de um cenário onde todas as manchas são ocupadas pela Larrea? Quanto tempo demora?
Distribuição Observada
Além de estimar a matriz de transição, no mesmo estudo, foi medida a frequência que cada um dos estados apresentava na natureza. Os dados obtidos foram os seguintes:
| Frequência observada | ||
|---|---|---|
| Estados | Aberto | 0,99854 |
| Ambrosia | 0,0013 | |
| Larrea | 0,00016 |
Compare os valores observados com o estimado pelo modelo matricial.
- Há correspondência entre o observado e o esperado pelo modelo?
- Qual o estado que pelo modelo se afasta mais do observado?
- Sugira uma possível explicação para esse desvio.
Bibliografia
Gotelli, N. 2007. Ecologia. Editora Planta. Londrina - Capítulo 8.
MacAuliffe, J.R. 1988. Markovian dynamics of simple and complex desert plant communities. The American Naturalist 131: 459-490.