Tabela de conteúdos
<script src="https://sagecell.sagemath.org/static/jquery.min.js"></script>
<script src="https://sagecell.sagemath.org/static/embedded_sagecell.js"></script>
<script>
sagecell.makeSagecell({inputLocation: '.groupone', linked: true, languages: ["maxima"]})
</script>
Growth rates and the exponential function - Tutorial in R
From discrete to continuous time
It may be more comfortable to think in changes in the population size in discrete intervals: we count the number of individuals at a given time, and repeat the count in the following time steps. This dynamic is described in the geometrical model, in which the population grows without bounds.
But how long do we wait between one census and another? If the births and deaths can occur at any time is a good idea to census the population on very short intervals. This script will show that the continuous time is just another way of thinking in discrete time: we make the intervals as small as we want. This will be our starting point to derive the exponential growth model, with the help of some computer tools.
Discrete time
Let's see the initial growth phase of a bacteria population in this video1):
<iframe width="640" height="360" src="http://www.youtube.com/embed/gEwzDydciWc?feature=player_embedded" frameborder="0" allowfullscreen></iframe>
Now let's try to describe the number of observed bacteria at every time interval:
| Time | N. of bacteria |
|---|---|
| 0 | 2 |
| 1 | 4 |
| 2 | 8 |
| 3 | 16 |
| 4 | 32 |
| 5 | 64 |
| … | … |
| 14 | 16384 |
| … | … |
| 30 | 1073741824 |
| … | … |
| 60 | 1152921504606846976 |
It may be hard to understand what's happening with just this table. A graph may help:
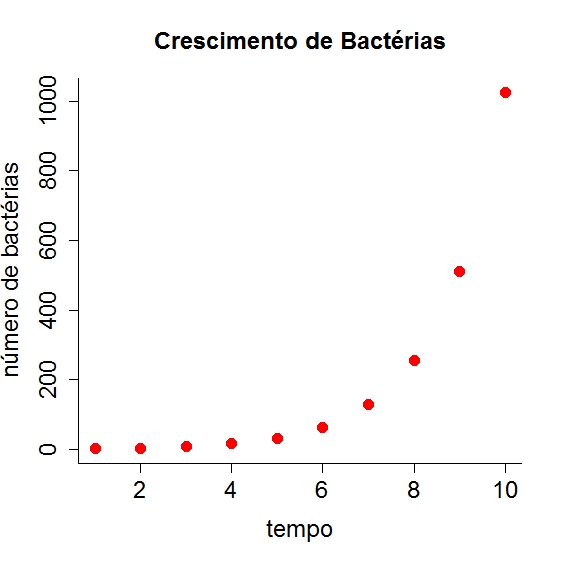
If you want to reproduce the plot
Open R and paste the code:
time=1:10 nbact= c(2,4,8,16,32,64,128,256, 512,1024) plot(time, nbact, main="Bacterial growth", ylab= "number of bacteria", pch=16, col="red",cex.main=1.5, cex=1.5,cex.lab=1.5, cex.axis=1.5,bty="l")
Notice that we have counts of the population size in discrete time intervals. Another way of describing this data is by asking
- How fast is the population growth or,
- What is the bacteria growth speed
Intuitive notion for derivatives
To express how much the population varies in a given time period, we can calculate the population variation rate from time $t$ to that time plus an interval $\Delta t$:
Variation rate $= \frac{{N(t + \Delta t) - N(t)}}{\Delta t} $
Or: take the number of bacteria in two times and divide the difference by the time elapsed.
But this $\Delta t$ is arbitrary. If the population has well-defined reproductive periods (i.e., annual), this observation interval may be a good choice. But what if births and deaths can occur at any point in time? The smaller our observation interval, the more precise will be our description of the population dynamics. In these cases, we should make the $\Delta t$ be as close to zero as we can.
But if we approach zero time interval, then ${N(t + \Delta t) - N(t)}$ should also go to zero, as the population sizes in both instants will be very close to each other. So the final result should be something like $0/0$?
Let's see if this logic is correct. First, suppose we have a population whose size is equal to the square of the elapsed time ( $N(t)= t^2 $ ), then let's reduce the value of $$\Delta t$$ to see what happens with the variation rate on time t=1:
## t=1 time=1 ##let's create a vector with the delta t values decreasing dt=c(0.5,0.1,0.01,0.001,0.0001,0.00001,0.000001) tdt=time+dt Nt=time^2 Ntdt=tdt^2 (Ntdt-Nt)/dt
Strangely, the values seem to converge to 2, and not to 0! Try it a few more times to other values of time.
Notice that the values converge in the following fashion when $\Delta t -> 0 $:
| t | ${N(t + \Delta t) - N(t)} / {\Delta t} $ |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
| 5 | 10 |
That means the instantaneous growth rate for $t^2$ is approximated by $2t$ when $\Delta t$ is near zero. We just found out the derivative of the function $N(t)=t^2$!
Definition of a derivative
The derivative of a function $X(t)$ is defined as its instantaneous growth rate, obtained by the limit of the variation rate:
$\frac{X(t + \Delta t) - X(t)}{\Delta t}$
when $\Delta t \to 0$ 2). One way to represent a derivative is in the notation of a rate over time:
$$\frac{dX}{dt} = \lim_{\Delta t \to 0} \frac{X(t + \Delta t) - X(t)}{\Delta t}$$
Exponential growth
A simple way of thinking about derivatives is that they represent instantaneous velocities. The speedometer of a car shows the derivative of its position! Thinking about this analogy, let's study the speed of growth of our bacteria:
| Time | N. of Bacteria | Speed |
|---|---|---|
| 0 | 2 | |
| 1 | 4 | 2 |
| 2 | 8 | 4 |
| 3 | 16 | 8 |
| 4 | 32 | 16 |
| 5 | 64 | 32 |
The bacteria double at each time interval. So, if the population doubles, the growth speed also doubles. If it is multiplied by 4, the speed will be multiplied by 4, and so on. That means that the growth speed is proportional to the population size.
As we're talking about instantaneous speeds, let's represent this proportionality with a derivative:
(1) $${dN}/dt= rN$$
Here, the constant of proportionality $r$ is called the population intrinsic growth rate, that is, how much each individual contributes to the instantaneous variation in the population size. This is the simplest population growth model.
This model is a differential equation, as it sets an equality relation between the derivative of a function (left size) and an algebraic expression on the right hand side of the equation. In other words, this model says some function for the population size $N$ has a derivative proportional to itself. A function that has this property is a solution for this equation. One such function is:
(2) $$N_t=N_0e^{rt} $$
This is the exponential growth function! Let's see how did we arrive here.
Solutions for differential equations
A first order differential equation is a relation between the derivative of a function and some mathematical expression. Solving one equation like this means finding some function whose derivative satisfies the proposed relation.
The problem is: there is no easy algorithm to find these functions. There are several rules and tables that relate the most common derivatives with the corresponding functions (the “antiderivatives”). Other than those, a lot of mathematical manipulation it is generally needed to express a differential equation in terms of those simple functions. Even then, it is not always possible to express the solution using a known function - what we call an analytic solution. We are lucky that the equation:
$$ \frac{dN}{dt}=rN $$
is so simple that the analytical solution exists. Even better, some computer programs are able to solve this type of equation. They are called CAS: Computer Algebra System, and Maxima ![]() is one of these programs, that can help us finding the solution for differential equations. You can find more help about this on the [en:ecovirt:roteiro:soft:tutmaxima|Introdução ao Maxima]].
is one of these programs, that can help us finding the solution for differential equations. You can find more help about this on the [en:ecovirt:roteiro:soft:tutmaxima|Introdução ao Maxima]].
Maxima solutions
Below, we are defining an object eq1 in Maxima to indicate that we want to solve the differential equation found above (the command for this is ode2):
<div class="groupone"><script type="text/x-sage">
eq1: diff(N(t),t)=r*N(t);
</script>
</div>
The first argument is the differencial equaition, the second one the dependent variable ($N(t)$) and the third one the independet variable ($t$):
<div class="groupone"><script type="text/x-sage">
ode2(eq1, N(t), t)
</script>
</div>
The result should be:
$ N(t)=c e^{rt} $
Here, $c$ is an unknown constant. The expression above satisfies the differential equation, for any given value of $c$, and this is all the antiderivative rules are able to give.
Initial conditions
If we want to single out one function, we need something more: the initial conditions for the system. Let's define the initial population size, $N_0$. This is the population size on time zero, and it may be substituted on the equation for exponential growth:
$$N_0 = c*e^{0} = c*1 = c$$
So, $c = N_0$, and finally we have a single function to represent our exponential growth:
$$ N_t= N_0 e^{rt} $$
The exponential function
##########################
#### Continous growth ####
##########################
n<- c(0:100, 200, 500,1000, 10000, 100000,1e+10)
N0 <- 2
rd1 <- 1
N1<-N0* (1+ rd1/n)^n
N1_N0= N1[length(N1)]/N0
plot(1:103, N1[1:103]/N0, type="l")
text(x=50, y=2.5, labels= paste("Maximum = ", N1[length(N1)/N0]))
N1_N0
Duplication time
Duplication time 3) is defined as the time neceessary to duplicate some quantity, given a constant growth rate. We can apply this concept to the time needed to a population with constant growth rate to double in size, or to calculate the time until a debt under fixed interests will double.
The solution is simple. Given the inicial value ($N_0$), the growth rate $r$ and the population size projected ($2N_0$), we solve the equation for time:
$$2N_0 = N_0e^{rt}$$
We just need some algebra, dividing both sides by $N_0$:
$$ e^{rt} = 2 $$
and then taking the natural logarithm for both sides:
$$ log(e^{rt}) = log(2) $$ $$ rt = log(2) $$ $$ t = \frac{log(2)}{r} $$
As $log(2)$ is approximately 0.7, we have:
$$ t_{dupl} \approx \frac{0,7}{r} $$
If growth rate is expressed in percentage, we have:
$$ t_{dupl} \approx \frac{70}{r_{\%}} $$
Exercises
Interests
A way to calculate compound interests from a loan 4) is through the exponential equation, were:
- r = interests
- N0 = loan
- Nt = debt
Uma dívida
- 10% per month
- 50% per year
- 0,5% per day
- Konwing that you will only be able to pay the debt in two years, calculate the money you will pay.
- Calculate the duplication time for any of the interests above.
More interests!
A new car
Imagine you receive a undergrad fellowship and decided to by a car. There are two options for you, both with fixed portions:
- price $ 27.000,00, interests 1.1% per month to pay after 100 months
- price $ 31.000,00, interests 0.7% per month to pay after 50 months
- Answer:
- What will be the final price of the car in both options?
- the price of the month protions;
- how many cars will you pay in both options?
- what is the duplication time in both options?
- what is your second career option?
Any similarity will be mere coincidence
According to the physicist Al Bartlett, one of the biggest tragedies of humanity is the incapacity to understand the consequences of constant growth rates. His speech about it is a classic, repeated more than 1600 times! Here, Prof Bartlett proposes the following problem:
To know more
- From the excelent learning site based in intuition Better Explained:
- History of numbers and, from The MacTutor History of Mathematics archive, University St Andrews.
- Exponential Function in wikipedia.
- Al Bartlett's website, with an excelent material about the consequences of grouwing populations and debts in constant interests.
R maxima calculo uma_população crescimento_exponencial tempo_discreto tempo_contínuo equação_diferencial
R maxima uma_população crescimento_exponencial tempo_discreto tempo_contínuo equação_diferencial


