−Tabela de conteúdos
Teoria neutra da biodiversidade - Roteiro no EcoVirtual
A Teoria Neutra é um modelo de processos estocásticos de nascimentos, mortes, especiações e migrações. As probabilidades de cada um destes eventos ocorrerem definem uma dinâmica surpreendente. A melhor maneira de entender isto é simular este processo, como faremos nos exercícios a seguir.
Preparação: entendendo caminhadas aleatórias
A Teoria Neutra usa uma classe de modelos de dinâmica estocástica, chamada caminhada aleatória de soma zero. Por isso precisamos entender algumas propriedades importantes dessa dinâmica.
Faça os tutoriais de caminhadas aleatórias, indicados nos links abaixo. Os conceitos apresentados nesses dois roteiros são centrais para o entendimento da Teoria Neutra. Apenas siga com este roteiro quando estiver certo(a) de que compreendeu os roteiros a seguir:
A Teoria passo a passo
Para prosseguir você deve ter o ambiente R com os pacotes Rcmdr e Ecovirtual instalados e carregados. Se você não tem e não sabe como ter, consulte a página de Instalação.
Caso já tenha o R e pacotes instalados
Carregue o pacote principal RcmdrPlugin.EcoVirtual pelo menu do R Pacotes > Carregar Pacotes, ou pela linha de comando com o código:
library("RcmdrPlugin.EcoVirtual")
Agora que entendemos algumas propriedades básicas de cadeias Markovianas simples vamos construir o modelo estocástico da Teoria Neutra, passo a passo, usando funções do EcoVirtual.
Dinâmica Local sem Migração
Vamos começar com um modelo para a comunidade em um dado local, usando um jogo de soma zero, similar ao jogo de apostas do roteiro de introdução a processos estocásticos que acabou de fazer1). As regras são:
- A comunidade tem um total fixo de indivíduos J que não se altera;
- Estes indivíduos pertencem a populações de um certo número S de espécies;
- Um dos indivíduos é sorteado para morrer
- Em seguida, os indivíduos remanescentes são sorteados, para definir quem produzirá o filhote que ocupará o lugar do indivíduo morto.
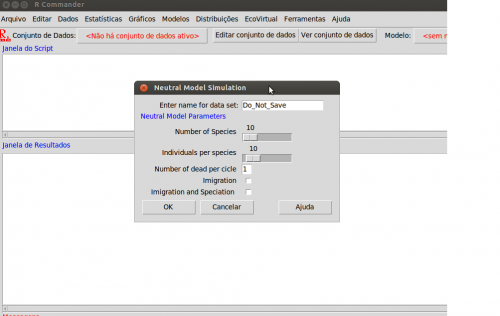
Para simular este processo, temos mais uma super-função no EcoVirtual. Vá em EcoVirtual > Biogeograph Models > Neutral Simulation… A seguinte janela de menu se abrirá:
com as seguintes opções:
| Opção | parâmetro | O que faz |
|---|---|---|
| Number of Species | S | número inicial de espécies |
| Individuals per Species | j | número inicial de indivíduos por espécies. Começamos com o mesmo número de indivíduos por espécie, portanto o tamanho da comunidade será J=Sj |
| Number of dead per cycle | D | número de mortes por ciclo 3) |
| Cycles per simulation | cycle | número de ciclos por simulação |
Simule uma comunidades com 100 espécies e 2 indivíduos por espécie:
- S = 100
- j = 2
Quando você não quiser mais ver a animação da dinâmica da comunidade é só desmarcar a caixa “Show simulation frames”.
Repita algumas vezes. O que acontece com o número de espécies com o passar do tempo? Verifique se isto muda aumentando o tamanho da comunidade, que é o produto Sj. Portanto basta manter o mesmo número de espécies e aumentar o número de indivíduos por espécie:
- S= 100
- cycles = 10.000
- j = 2 a 12, a intervalos de 2
Questões
- Para qual número de espécies tende uma comunidade fechada sob dinâmica neutra?
- Qual o efeito do tamanho da comunidade sobre a taxa de perda de espécies?
Incluindo Migrações
 Sabemos que as comunidades não são sistemas fechados. Então a chegada de migrantes pode compensar a perda de espécies que observamos na simulação anterior. Vamos supor, então, que há um reservatório externo de migrantes, que chamamos metacomunidade. Uma maneira bem simples de se fazer isto é supor uma metacomunidade infinita, com todas as espécies do início da simulação, nas proporções iniciais. Precisamos definir também a taxa de migração: ela será a probabilidade de um indivíduo morto na comunidade ser substituído por um propágulo vindo de fora, da metacomunidade.
Sabemos que as comunidades não são sistemas fechados. Então a chegada de migrantes pode compensar a perda de espécies que observamos na simulação anterior. Vamos supor, então, que há um reservatório externo de migrantes, que chamamos metacomunidade. Uma maneira bem simples de se fazer isto é supor uma metacomunidade infinita, com todas as espécies do início da simulação, nas proporções iniciais. Precisamos definir também a taxa de migração: ela será a probabilidade de um indivíduo morto na comunidade ser substituído por um propágulo vindo de fora, da metacomunidade.
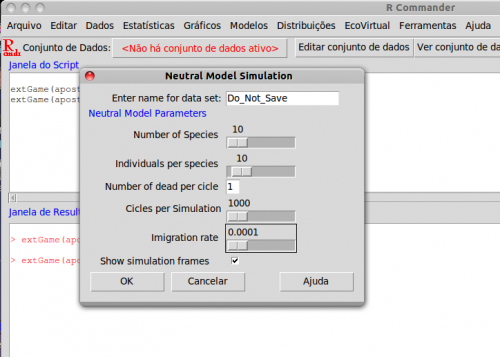
Marque a opção 'Imigration' na janela da simulação de Neutral Model Simulation (a mesma da figura anterior) do menu EcoVirtual e clique em OK, janela abrirá a opção do valor de imigração:
Compare a dinâmica de número de espécies ao longo do tempo em comunidades sem migração, e com valores crescentes de taxa de migração. Para isso experimente valores de migração (Immigration (m)) de zero a 0,5. Em todos comece com uma comunidade com 100 espécies, com dois indivíduos por espécies, e mantenha constante o número de ciclos em todas as simulações:
- S = 100
- j = 2
- cycles = 10.000
- m = 0 a 0,5, a passos de 0,1
Questões
- Para qual número de espécies uma comunidade com dinâmica neutra e imigrações tende, dado tempo suficiente?
- Qual o efeito de aumento da imigração sobre o estado final da comunidade?
- O que acontece se aumentamos o tamanho da comunidade? Dica: experimente simular com uma mesma taxa de migração e vários tamanhos de comunidade, começando com 10 indivíduos por espécie.
Uma Metacomunidade mais Realista
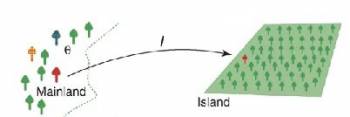
Um reservatório infinito de espécies não parece ser uma premissa muito realista. Que tal substituí-lo por um conjunto de populações com a mesma dinâmica que usamos para a comunidade? Teríamos, então, dois sistemas acoplados, cada um com sua dinâmica estocástica de nascimentos e mortes.
Mas se a metacomunidade também segue a dinâmica estocástica de soma zero, também perderá espécies com o tempo. Como resolver? Começamos por admitir que a metacomunidade é muito maior que a comunidade, pois representa o pool regional de colonizadores. Ou seja, é um sistema bem maior, pois tem mais espécies e indivíduos. Vamos supor, muito modestamente, que nela há o dobro de espécies da comunidade, cada uma com dez vezes mais indivíduos.
Apenas para lembrar o efeito do tamanho da comunidade sobre a erosão de espécies, use novamente a função de simulação sem migração para comparar sistemas que diferem nesta ordem de grandeza:
- S = 100
- cycles = 20.000
- j = 2 e 20
Já é possível perceber que para tamanhos razoáveis (ou mesmo pequenos) de metacomunidades a erosão de espécies é bem lenta. Portanto, uma entrada de espécies a uma taxa também muito lenta já seria suficiente para compensar as extinções. Se for tão lenta quanto o tempo necessário para a evolução de uma nova espécie no sistema já temos a solução: na metacomunidade, as espécies perdidas são repostas por novas que surgem, no tempo evolutivo!
Assim, definimos uma taxa de especiação, ν, que expressa a probabilidade de um indivíduo morto na metacomunidade ser reposto por um indivíduo de uma nova espécie. Esta taxa é extremamente baixa, mas pode ser suficiente para manter, ou mesmo elevar, o número de espécies na metacomunidade.
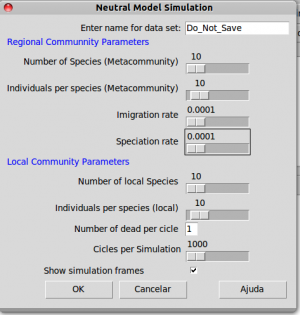
Vamos ver como isso é feito no EcoVirtual. Vá novamente ao submenu Biogeographical models do menu EcoVirtual e selecione Neutral Simulation. Na janela de opções aberta, selecione a opção imigration and speciation em seguida clique em OK.
Agora temos argumentos também para os parâmetros da metacomunidade:
| Opção | parametro | O que faz |
|---|---|---|
| Number of Species (Metacommunity) | Sm | número de espécies da metacomunidade |
| Individuals per Species (Metacommunity) | jm | número de indivíduos por espécie na metacomunidade |
| Speciation rate | nu | taxa de especiação na metacomunidade |
| Migration rate | m | taxa de migração na metacomunidade |
Usando os tamanhos de comunidades e metacomunidades que já definimos, avalie o efeito de aumentar a taxa de migração, mantendo os outros parâmetros constantes:
- S = 100
- j = 2
- Sm = 200
- jm = 20
- nu = 1×10−9
- m = 0 a 0,4 a intervalos de 0,1
Mais algumas explorações
Experimente também variar os tamanhos da comunidade e da metacomunidade, e a taxa de especiação.
Outra boa idéia é aumentar o tempo das simulações, para avaliar a dinâmica a longo prazo. Para isto, aumente o valor do argumento cycle, mas lembre-se que com valores muito altos a simulação podem demorar. Tenha paciência 4)!!
O modelo de Hubbell permite o cálculo do Número fundamental da biodiversidade, expresso por θ (theta) nos gráficos. Essa é uma medida da diversidade da metacomunidade (alfa de Fisher regional5)) e está relacionada à taxa de especiação e ao tamanho da metacomunidade.
Questões
- Em escala de tempo ecológico a metacomunidade desta simulação tem efeito muito diferente da metacomunidade fixa e infinita da simulação anterior?
- Qual o efeito de uma maior taxa de especiação na metacomunidade sobre a dinâmica da metacomunidade?
- O que acontece se a metacomunidade é muito pequena?
Para saber mais
Introduções
- Harpole, W. (2010) Neutral Theory of Species Diversity. Nature Education Knowledge 3(10):60. Ótima apresentação da teoria, do projeto Scitable.
- Cassemiro, F.A.S. & Padial, A.A. 2008. Teoria Neutra da Biodiversidade: aspectos teóricos, impacto na literatura e perspectivas. Oecologia Brasiliensis, 12 (4): 706-719 disponível online aqui.
- Alonso, D., R. S. Etienne, and A. J. Mckane 2006. The merits of neutral theory. Trends in Ecology & Evolution 21: 451-457.
- Um pacote em R para simulação e ajuste dos modelos de distribuição de espécies previstos pela teoria. A introdução é uma excelente explicação da teoria:
- Hankin, R. 2007. Introducing untb, an R Package For Simulating Ecological Drift Under the Unified Neutral Theory of Biodiversity. Journal of Statistical Software 22: 12 http://www.jstatsoft.org/v22/i12/.
Mais avançadas
- O livro (referência básica, mas nem sempre didática quanto ao modelo):
- Hubbell, S.P. (2001). The Unified Neutral Theory of Biodiversity and Biogeography. Princeton University Press.
- Rosindell, J., Hubbell, S. P. & Etienne, R. S. 2011. The Unified Neutral Theory of Biodiversity and Biogeography at Age Ten. Trends in Ecology & Evolution 26:340-348. Ótima revisão sobre o tema e seu impacto.
- Renshaw, E. 1991. Modelling biological populations in space and time Cambridge University Press. Excelente apresentação de dinâmicas estocásticas.
- Uma boa revisão da evidência empírica até a época, com comparações com outros modelos neutros: Brian J. McGill, Brian A. Maurer, Michael D. Weiser (2006) EMPIRICAL EVALUATION OF NEUTRAL THEORY. Ecology: Vol. 87, No. 6, pp. 1411-1423.