Tabela de conteúdos

Taxas de crescimento e função exponencial - Roteiro em R

fastest_growing.png

Este roteiro é uma demonstração informal dos principais passos de dedução do modelo de crescimento exponencial, a partir do modelo de crescimento a intervalos discretos. Você vai descobrir que a função exponencial é o limite de um crescimento discreto a uma taxa constante, quando fazemos os intervalos de tempo muito pequenos. Para isso, passaremos pelo conceito de derivadas e pela noção de limite de uma função.

Ao final, chegaremos a um dos primeiros princípios em ecologia: na ausência de forças externas, uma população biológica vai crescer ou descrescer exponencialmente. Infelizmente, juros também se comportam assim.

Do tempo discreto para o contínuo

Para muitos parece mais confortável pensar em mudanças no tamanho da população a intervalos discretos: contamos o número de indivíduos em um instante e no instante seguinte. O modelo geométrico descreve esta dinâmica, se a população cresce sem limites. O número de indivíduos no próximo intervalo de tempo, $N_{t+1}$, é igual ao número de indivíduos no tempo anterior $N_t$, multiplicado pela taxa de crescimento da população entre os dois intervalos, que chamamos $\lambda$:

$$N_{t+1} \ = \ \lambda N_t$$

Mas quanto esperamos entre uma contagem e outra? Se os nascimentos e mortes podem ocorrer a qualquer momento, devemos fazer censos a intervalos bem curtos. Mostraremos que o tempo contínuo é apenas uma outra maneira de pensar no tempo discreto: tornamos os intervalos tão pequenos quanto quisermos. Esse será nosso ponto de partida para deduzir o modelo de crescimento exponencial, com auxílio de algumas ferramentas computacionais.

Tempo discreto

Vamos acompanhar o crescimento inicial e uma população e bactérias no vídeo 1):

O que pode ser descrito pelo número de bactérias observadas a cada intervalo de tempo:

TempoNo. de Bactérias
0 2
1 4
2 8
3 16
4 32
5 64
……
14 16384
… …
30 1073741824
……
601152921504606846976

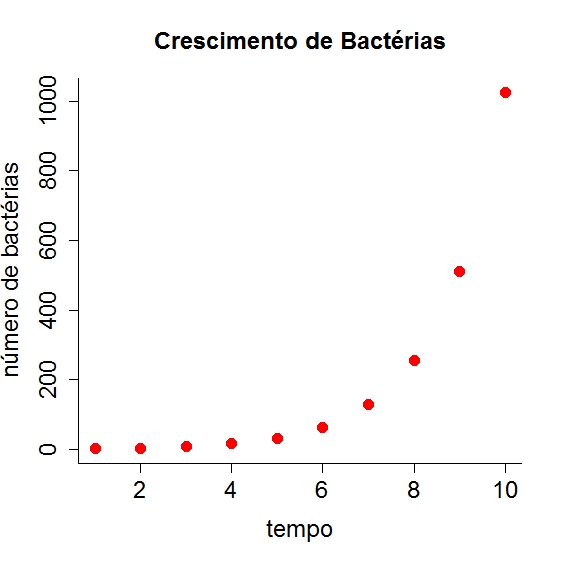
É difícil entender o que está acontecendo, apenas olhando essa tabela. Um gráfico pode ajudar.

nbact.jpg

Se quiser reproduzir este gráfico

Abra o R e cole o código abaixo, linha a linha: 

tempo=1:10
nbact= c(2,4,8,16,32,64,128,256, 512,1024)
plot(tempo, nbact, main="Crescimento de Bactérias", ylab= "número de bactérias", pch=16, col="red",cex.main=1.5, cex=1.5,cex.lab=1.5, cex.axis=1.5,bty="l")

Pronto, vc. já simulou os dados do crescimento. Agora é só fazer o gráfico. Veja se consegue fazer parecido com o que apresentamos acima. Em seguida faça um outro gráfico com o tempo chegando a 20.

Note que o que temos é uma série temporal, que são registros do tamanho da população em certos instantes de tempo. Uma outra forma de descrever esse processo é saber:

  • Quão rápido cresce o número de bactérias ou,
  • Qual a velocidade de crescimento das bactérias

A noção de derivada

Para expressar o quanto a população variou em um dado período de tempo calculamos a taxa de variação da população no tempo $t$ e após um intervalo $\Delta t$:

$$\text{Taxa de Variação}= \frac{{N(t + \Delta t) - N(t)}}{\Delta t} $$

Ou seja: tome os valores do número de bactérias em dois tempos próximos e divida pelo tempo decorrido entre uma observação e outra!

Entretanto o $ \Delta t $ é arbitrário. Se a população tem períodos reprodutivos bem definidos (p.ex. anuais), o intervalo de observação discreto é natural. Mas e se nascimentos e mortes podem ocorrer a qualquer momento? Quanto menores nossos intervalos de observação, mais precisa será a nossa descrição da dinâmica. Nestes casos parece uma boa ideia fazer o intervalo $\Delta t$ ser o menor possivel, bem próximo de zero.

Mas se aproximamos $\Delta t$ de zero, ${N(t + \Delta t) - N(t)}$ tenderia também a zero, já que os tamanhos populacionais nos dois momentos seriam muito parecidos. Portanto o resultado dessa taxa deve ser $0/0$ 2).

Vamos verificar se essa lógica está correta. Para começar, vamos supor uma população cujo tamanho é igual ao quadrado do tempo decorrido ( $N(t)= t^2 $ ) 3). Vamos então aplicar esta função para intervalos cada vez menores de tempo a partir de t=1, e ver o que acontece para a taxa de variação do tamanho populacional: 

## para t=1
tempo=1
##vamos criar um vetor com valores de delta t diminuindo
dt=c(0.5,0.1,0.01,0.001,0.0001,0.00001,0.000001)
tdt=tempo+dt
Nt=tempo^2 
Ntdt=tdt^2
(Ntdt-Nt)/dt

Ao contrário do que esperávamos, o valor da taxa converge para um número bem definido com a redução de $\Delta t$ !

Repita o procedimento para outros valores tempo. Você deve encontrar este resultado:

t ${N(t + \Delta t) - N(t)} / {\Delta t} $
1 2
2 4
3 6
4 8
5 10

Ou seja, a taxa instantânea de crescimento para $t^2$ tende a $2t$ à medida que $\Delta t$ é reduzido. Podemos reduzir $\Delta t$ o quanto quisermos, e este resultado fica cada vez mais exato. Encontramos a derivada da função $N(t)=t^2$ !

Definição de uma derivada

A derivada de uma função $X(t)$ é sua taxa de variação instantânea, obtida pelo limite da taxa de variação:

$$\frac{X(t + \Delta t) - X(t)}{\Delta t}$$

quando $\Delta t \to 0$ 4). Uma das maneiras de representar uma derivada é na notação de uma taxa em relação ao tempo:

$$\frac{dX}{dt} = \lim_{\Delta t \to 0} \frac{X(t + \Delta t) - X(t)}{\Delta t}$$

Crescimento Exponencial

Uma maneira simples de pensar em derivadas é que elas são velocidades instantâneas 5). Vamos então descobrir a expressão para a velocidade instantânea de crescimento da nossa população de bactérias:

TempoNo. de BactériasVelocidade
0 2
1 4 2
2 8 4
3 16 8
4 32 16
5 64 32

As bactérias duplicam-se a cada instante de tempo. Por isso, se a população dobrar, a sua velocidade de crescimento também dobra. Se ela quadruplicar, a velocidade quadruplicará, e assim por diante. Ou seja, a velocidade de crescimento é proporcional ao tamanho da população.

Já que estamos interessados em velocidades instantâneas, vamos representar esta proporcionalidade com uma derivada: \begin{equation} \frac{dN}{dt}= rN \label{dndt} \end{equation}

Em que a constante de proporcionalidade $r$ é chamada taxa intrínseca de crescimento populacional, ou seja, o quanto cada indivíduo contribui instantaneamente para a variação no tamanho da população. Este é o modelo mais simples de crescimento populacional. O modelo é uma equação diferencial, pois estabelece uma igualdade entre a derivada de uma função (lado esquerdo) e alguma expressão algébrica, no lado direito da equação. Traduzindo em palavras, este modelo seria “uma função do crescimento populacional $N$ tem derivada proporcional a ela mesma”. A função que tem esta propriedade, ou seja, que satisfaz esta equação é:

\begin{equation} \label{ert} N_t=N_0e^{rt} \end{equation}

Que é a função de crescimento populacional exponencial. Vamos ver como chegamos a isso!

Soluções de equações diferenciais

Uma equação diferencial de primeira ordem estabelece uma relação entre a derivada de uma função e alguma outra função matemática. Resolver uma equação destas é encontrar a função cuja derivada satisfaça a relação proposta.

O problema é que não há um algoritmo simples para fazer isso. Há muitas regras e tabelas que relacionam derivadas mais simples às suas respectivas funções (as antiderivadas). Além disso, em geral é preciso muita manipulação matemática para expressar a equação diferencial em termos destas formas catalogadas. Mesmo assim, nem sempre se chega a uma solução que pode ser expressa como uma função conhecida, o que chamamos de solução analítica. Felizmente, a equação diferencial ($\ref{dndt}$) é simples o bastante para ter solução analítica conhecida.

Melhor ainda, hoje há programas de computador que manipulam regras de matemática simbólica, incluindo as antiderivadas que precisamos para resolver equações diferenciais. São os Sistemas de Álgebra Computacional6). O Maxima é um desses programas, e pode nos ajudar a solucionar a equação diferencial. Vamos usá-lo online.

As janelas de código abaixo executam o Maxima online: o código é enviado ao servidor Sage Cell, que tem o Maxima pronto para executar comandos. O servidor então retorna o resultado para nossa página.

Se preferir, você pode instalar o Maxima em seu computador e executar os mesmos comandos. É uma ferramenta muito útil para resolver problemas matemáticos. Veja nossa Introdução ao Maxima.

Solução no Maxima

O comando abaixo define um objeto chamado eq1 no Maxima, para armazenar a expressão simbólica da nossa equação diferencial $dN/dt=rN$. Clique no botão Evaluate para criar o objeto:

Agora use o comando ode2 do Maxima para resolver a equação diferencial. O primeiro argumento é a equação diferencial, o segundo a variável dependente ($N(t)$) e o terceiro a variável independente ($t$):

O resultado deve ser:

$$ N(t)=c e^{rt} $$

Onde $c$ é uma constante de integração desconhecida. A expressão acima satisfaz a equação diferencial, para qualquer valor de $c$, e isso é tudo que as regras de antiderivação podem nos dar.

Condições iniciais

Para ir adiante temos que dar algo mais: as condições iniciais do sistema. Vamos então definir o número inicial de indivíduos na população, $N_0$. Este é o tamanho da população no tempo zero, que substituímos na equação de crescimento exponencial:

$$N_0 = c*e^{0} = c*1 = c$$

Logo $c = N_0$, e finalmente temos nossa equação de crescimento exponencial:

$$ N_t= N_0 e^{rt} $$

A função exponencial

Satisfeito(a)? Espero que não, pois simplesmente apelamos para uma tabela de antiderivadas em um programa para encontrar a solução de nossa equação diferencial. Aprendemos a lógica geral da solução de uma equação diferencial, mas não porque a equação que propusemos tem esta solução específica.

Uma maneira de entender é retornar ao raciocínio de reduzir intervalos de tempo. Vamos começar com uma população que tem uma taxa de crescimento anual de $\lambda = 1,5$:

Agora, vamos supor que essa mesma população tenha dois ciclos reprodutivos anuais, portanto temos que calcular o aumento na população no primeiro semestre do ano, e multiplicar este valor novamente pela taxa de crescimento, para obter o tamanho da população no final do ano. Vamos supor que a taxa semestral de crescimento seja metade da anual:

$$N_1 \ = \ N_0 \left( 1+\frac{0,5}{2} \right) \left( 1+\frac{0,5}{2} \right)$$

Isso equivale a

$$N_1 \ = \ N_0 \left( 1+\frac{0,5}{2} \right)^2 \ = \ N_0(1+0,25)^2 \ \to \frac{N_1}{N_0} \ = \ (1+0,25)^2 \ \simeq \ 1,56$$

Ops! Uma taxa de crescimento de 1,25 ao semestre resulta em um crescimento maior que a taxa anual de 1,5. Não é difícil entender: no segundo semestre a população aumentou em 25% de uma população que já cresceu 25% no primeiro semestre. Mantendo o raciocínio, trimestralmente a taxa seria de $(1 + 0.5/4)$ e deveria ser aplicada quatro vezes. Isso resultaria em um crescimento anual de cerca de 1,60. Onde isso vai parar?

Jacob Bernoulli foi o primeiro a solucionar este problema, preocupado com o comportamento de juros compostos, nos idos do século XVII. Ele partiu da expressão usada para calcular estes juros, que nada mais é que a generalização de nossa expressão de crescimento em um ano dividido em n intervalos, :

$$ \frac{N_1}{N_0}= \left( 1+\frac{r_d}{n} \right) ^n $$

Em seguida ele notou que para calcular uma dívida (o tamanho da população em nosso caso) que aumenta a todo instante, teríamos que deixar o número de intervalos de tempo ($n$) cada vez maior, tendendo a um número infinitamente grande:

$$ \lim\limits_{n \to \infty} \left( 1+\frac{r_d}{n} \right)^n$$

Isto é o mesmo que fazer os intervalos de tempo serem infinitamente pequenos. O que acontece então? Vamos tentar resolver o limite numericamente no R, aumentando o número de divisões dentro de um ano da nossa taxa de crescimento discreta. A princípio vamos deixar o $\lambda =2$, portanto o $r_d=1$ e o $N_0=1$ ; portanto $\frac{N_t}{N_0}= N_t$. Em seguida vamos fazer $\lambda =3$ e $\lambda =1.5$ (r=2 e r=0.5). 

##############################
#### Crescimento Contínuo ####
##############################

n<- c(0:100, 200, 500,1000, 10000, 100000,1e+10)
N0 <- 2
rd1 <- 1  
N1<-N0* (1+ rd1/n)^n
N1_N0= N1[length(N1)]/N0
plot(1:103, N1[1:103]/N0, type="l")
text(x=50, y=2.5, labels= paste("Máximo = ", N1[length(N1)/N0]))
N1_N0

Tempo de Duplicação

Tempo de duplicação 7) é definido como o tempo necessário para uma quantidade duplicar, dada uma taxa constante de crescimento. Podemos aplicar este conceito para o tempo necessário para que uma população com taxa constante de crescimento dobre de tamanho, ou para o tempo até que uma dívida sob taxa fixa de juros dobre de valor.

A solução da expressão de tempo de duplicação é simples. Dados o valor inicial ($N_0$), a taxa de crescimento $r$ e o tamanho da população projetada ($2N_0$), resolvemos equação para o tempo:

$$2N_0 = N_0e^{rt}$$

Para isso precisamos de um pouco de álgebra apenas. Dividimos os dois lados da equação por $N_0$:

$$ e^{rt} = 2 $$

e em seguida tomamos o logarítmo em base natural dos dois lados da equação

$$ log(e^{rt}) = log(2) $$ $$ rt = log(2) $$ $$ t = \frac{log(2)}{r} $$

Como $log(2)$ é aproximadamente 0,7 8), temos:

$$ t_{dupl} \approx \frac{0,7}{r} $$

Se a taxa de crescimento estiver expressa em percentual, como é comum para juros, temos :

$$ t_{dupl} \approx \frac{70}{r_{\%}} $$

Exercícios

Juros

Uma forma para calcular juros composto de um empréstimo 9) é através da equação exponencial, similar à apresentada acima, onde:

  • r = juros
  • N0 = valor emprestado
  • Nt = valor final

pateta_escola_escrevendo.gif

Uma dívida

Você precisa de 1000 reais emprestados e suas opções em diferentes bancos são:
  • 10% ao mês
  • 50% ao ano
  • 0,5% ao dia
  1. Sabendo que só poderá pagar a dívida daqui a dois anos (à vista), calcule o valor que irá desembolsar.
  2. Calcule o tempo de duplicação para cada uma das taxas de juros acima.

Mais juros!

pateta_carro.jpg

Um carro novo

Imagine que é bolsista PIBIC do Departamento de Ecologia da USP (tinha que ter algo de ecologia no exemplo!) e resolveu comprar um carro. Há duas opções que parecem caber no seu bolso de um carro básico (sem ar, direção e freios), ambos com parcela fixas:

  1. valor à vista de R$ 27.000,00 com juros de 1,1% ao mês e pagamento após 100 meses
  2. valor à vista de R$ 31.000,00 com juros de 0,7% ao mês e pagamento após 50 meses
  • Responda:
    1. Qual o valor final do carro em cada uma das opções;
    2. o valor das prestações;
    3. quantos carros vc. estaria pagando em cada caso?
    4. qual o tempo de duplicação de cada opção?
    5. qual sua segunda opção de profissão?

Qualquer semelhança será mera coincidência

Segundo o físico Al Bartlett, uma das maiores tragédias da humanidade é a incapacidade de compreender as consequências de taxas de crescimento constantes. Sua palestra sobre o tema é um clássico, proferida mais de 1600 vezes! Nesta palestra o Prof Bartlett propõe o seguinte problema:

Era uma vez uma civilização de bactérias que vivia em uma garrafa de um litro. A população crescia a uma taxa constante tal que o tempo de duplicação era de um dia. A população crescia e a civilização prosperava, até que a garrafa encheu. Nesse momento, metade das bactérias cessou a reprodução e partiu em busca de outra garrafa, para evitar um desastre demográfico. Assim que encontraram uma nova garrafa de um litro se instalaram e retomaram a mesma taxa de crescimento, tão aliviadas quanto as suas companheiras que ficaram na garrafa original, também crescendo à mesma taxa. Quanto tempo durará o alívio?

Para saber mais

, , , , , ,
1)
Caso o vídeo não esteja disponível na sua página entre nesse link
2)
um horror matemático! Veja aqui
3)
Este não é o modelo biologicamente mais adequado para crescimento de populações, mas é mais didático para entendermos derivação. Depois passaremos ao modelo de crescimento discreto, fique tranquilo(a)
4)
o que se lê “quando $\Delta t$ tende a zero”, ou seja, aproxima-se de zero tanto quanto você quiser.
5)
o velocímetro de um carro mostra derivadas
6)
em inglês CAS, Computer Algebra System
7)
veja: http://en.wikipedia.org/wiki/Doubling_time
8)
com sete casas decimais = 0,6931472
9)
esse exemplo é simplificado, em geral os juros são calculados pelo saldo e não pela dívida inicial