Determine o resultado das seguintes integrações:

a) $ \int \sin(x) dx$

b) $ \int x^2 +1 dx$

c) $ \int _0^1 \cos (x) dx$

d) $ \int _{-1}^5 x^3 +2x dx$

e) $ \int _1 ^ \infty \frac{1}{x^2}dx$

f) $ \int _0 ^ 1 \sin ( x^{27} ) dy $ (cuidado, pegadinha!)

Quais desses são integrais definidas e quais são integrais indefinidas?

(Use o Maxima)

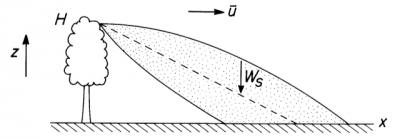
Em algumas espécies o principal fator que leva a dispersão das sementes é o vento. É possível modelar a distribuição das sementes em função da distancia da fonte mecanisticamente, e uma das expressões, para ventos unidirecionais, que podem ser derivadas é

* $ Q(x) = \frac{NW_s}{\sqrt{2\pi}\bar u \sigma_z} \exp \left[ - \frac{ (H-W_sx/\bar u)^2 } {2 \sigma_z^2} \right] $

Os parâmetros dessa equação são:

* $N$: a taxa de produção de sementes na fonte

* $\sigma_z$: o componente vertical da variância no movimento aleatório da semente

* $W_s$: a velocidade de fixação da semente

* $\bar u$: velocidade media do vento

* $H$: altura da fonte

(Okubo & Levin, 1989)

1) Vamos encontrar qual é o total de sementes que uma árvore dispersa em um raio de 1m. Para isso, integre a função $Q(x)$ entre -1 e 1. Use $N = 100$, $\sigma_z = W_s = \bar u = H = 1$.

2) Qual é o total de sementes dispersadas em todo o eixo x? Esse resultado é esperado?

3) Qual é a expressão que, para uma certa distancia $d$, dá o total de sementes dispersadas entre 0 e $d$?

* (Nota: ERF? Leia sobre essa função esquisita aqui )

No exercicio 2, consideramos a dispersão de sementes no espaço em um tempo fixo (como uma fotografia). Vamos agora observar a produção de sementes ao longo do tempo: agora $N$ sera uma função periódica do tempo para representar as estações do ano:

* $ N(t) = N_0(\sin(t) + 1) $

Vamos usar $N_0 = 100$, e assim, nosso exercício anterior corresponde ao caso em que $\sin(t)=0$ (por exemplo, com $t=0$).

Agora, nossa função $Q(x, t)$ depende não só de $x$, mas também de $t$:

$ Q(x, t) = \frac{N(t)W_s}{\sqrt{2\pi}\bar u \sigma_z} \exp \left[ - \frac{ (H-W_sx/\bar u)^2 } {2 \sigma_z^2} \right] $

1) Encontre a densidade total de sementes dispersadas na distância entre -1 e 1 no tempo 0, para se certificar de que isso bate com o resultado anterior: $\int _{-1}^1 Q(x, 0) dx$.

2) Qual é a densidade de sementes que caem sobre o ponto $x=1$ durante um ciclo anual completo, ou seja, com $t$ variando de 0 a $2 \pi$? Resolva a integral no tempo: $ \int _0 ^ {2 \pi} Q(1, t) dt$.

3) Encontre uma expressão para a densidade de sementes em momento $t$ qualquer, no raio de x entre -1 e 1. Veja que essa resposta vai ser uma função de t, vamos chama-la de $h(t)$, onde $h(t) = \int _{-1}^1 Q(x,t) dx$.

4) Use essa função que você achou na questão 2.3 para encontrar a densidade total de sementes dispersadas com x entre -1 e 1 e durante todo um ciclo anual.

Nesse último exercício, você calculou a integral $ \int _0 ^ {2 \pi} h(t) dt$. Se você escrever a definição de $h(t)$ nessa expressão, vamos chegar a:

$ \int _0 ^ {2 \pi} \int _{-1} ^ 1 Q(x, t), dx dt $

Parabéns! Você acabou de fazer uma integral dupla!

(Não precisa entregar essa parte, mas leia com carinho!)

1) Na questao 2 acima, a nossa produção de sementes está posicionada na origem. Se uma árvore estiver em uma posição genérica x, escreva qual é a expressão da taxa de queda de sementes em um ponto y.

2) Mudemos agora nosso ponto de vista. Numa expedição de reconhecimento matemático pelo eixo x, intrépidos exploradores encontraram uma vasta e densa floresta, que se estende do ponto A ate o longínquo ponto B, composta por N fontes de sementes homogeneamente distribuídas. É possível construir uma função que nos dê a taxa de queda de sementes em cada ponto do eixo? (Como temos um modelo de vento unidirecional, suponha que venta de A para B)

3) É possível quantificar a taxa de emigração dessa floresta (a taxa de sementes que se fixam para além de B)?

4) Como ficaria a expressão construída em 2 se a floresta, ao invés de ser homogênea, tivesse suas fontes distribuídas seguindo uma normal?

5) E se ventasse metade do tempo para cada lado, como ficaria a expressão em 2?

6) Usando a expressão obtida em 5, e o teorema fundamental do cálculo, descubra o ponto em que se fixa o maior numero de sementes.

Veja a solução do exercício solexintegral.wxm