−Tabela de conteúdos
ATENÇÃO: ESTA PÁGINA É UMA VERSÃO ANTIGA DO ROTEIRO E ESTÁ DESATIVADA, PARA ACESSAR O ROTEIRO ATUAL ACESSE ESTE LINK
Crescimento denso-independente com estocasticidade demográfica - Roteiro no Ecovirtual
Os modelos determinísticos de dinâmica populacional não consideram a variação de aptidão entre os indivíduos. Por exemplo, quando usamos o modelo de crescimento discreto
Nt+1=1,5×Nt
supomos que a cada intervalo de tempo o saldo médio entre nascimentos e mortes é de três para dois, causando um crescimento de 50% na população. Isso poderia acontecer se metade dos indivíduos morrer sem deixar descendentes e a outra metade sobreviver e tiver dois filhotes, cada. Também é possível se todos morrerem, mas apenas um ter 1,5×Nt filhotes antes.
O raciocínio é o mesmo para outros modelos determinísticos. No modelo de crescimento exponencial N(t)=N0ert por exemplo, a população cresce por um fator de ert, devido à taxa de crescimento instantânea r, que nada mais é que o saldo das taxas de nascimentos e mortes.
Em resumo, as taxas populacionais são médias que resultam de uma infinidade de arranjos de mortes e nascimentos na população, a maioria com variação de aptidão. A simples natureza fracionária das taxas já implica em variação. Por exemplo, uma taxa de natalidade de 0,5 indivíduo/indivíduo.ano indica que alguns se reproduzem e outros não, pois filhotes não vêm em metades!
A estocasticidade demográfica é o efeito da variação de aptidão individual sobre a dinâmica populacional. O objetivo desse roteiro é entender a lógica de construção de modelos de dinâmica populacional com esses efeitos, e conhecer suas principais propriedades.
Apenas mortes
Vamos começar com uma população de N0 indivíduos em que não há nascimentos nem migrações. As mortes ocorrem a uma taxa instantânea per capita de μ=0,693 ano−1. O modelo mais simples para calcular os tamanhos dessa população no tempo é o exponencial:
N(t)=N0e(nascimentos−mortes)t = N0e−0,693t
que para essa taxa de mortalidade prevê que a população é reduzida à metade a cada ano1).
Para isso acontecer, metade do indivíduos deve morrer e a outra sobreviver. Isso quer dizer que a taxa de mortalidade não é a mesma para todos? Para manter essa premissa de homogeneidade (e nosso modelo simples) podemos dizer que a probabilidade de morrer é igual para todos. No caso, todos os indivíduos têm 50% de chance de sobreviver ao próximo ano. Se começamos com N0=100, após um ano em média teremos 50, após dois 25 e assim por diante, exatamente como prevê o modelo exponencial.
Mas algo importante mudou em nosso modelo: agora o acaso faz o tamanho populacional variar em torno da média, por exemplo:
Vamos supor que temos apenas dois indivíduos. Cada um deles tem 50% de chance sobreviver ao próximo ano. Assumindo que as probabilidades são independentes, há três resultados possíveis2):
- Os dois indivíduos morrem, com probabilidade 0,5×0,5=0,25
- Um indivíduos morre e o outro sobrevive, com probabilidade 2×0,5×0,5=0,53)
- Os dois indivíduos sobrevivem, com probabilidade 0,5×0,5=0,25
Isso mostra que em nosso modelo estocástico4) há mais de um valor possível para a população no futuro. Portanto, agora temos incerteza nas projeções, que pode ser muito grande. Em nosso exemplo de uma população com dois indivíduos, a chance de termos o valor esperado é de apenas 50%!
Mas nada de pânico. Nosso exemplo também mostra que a incerteza é mensurável: é possível calcular a probabilidade de cada tamanho populacional ocorrer. No caso da nossa dinâmica apenas com mortes, a probabilidade de um indivíduo sobreviver até o tempo t é:
Probabilidade de Sobreviver p(t)=e−μt
Assim, esperamos ter p(t)N0 no tempo t, ou seja, o tamanho esperado da população5) continua o mesmo do modelo sem estocasticidade:
E[N(t)] = p(t)N0 = N0e−μt
O que mostra que em média o modelo com estocasticidade resulta nas mesmas projeções do modelo determinístico. Mas quanta variação há em torno dessa média? Ou seja, qual a chance de outros valores ocorrerem?
Distribuição de probabilidades dos tamanhos populacionais
Como calcular a chance de cada tamanho populacional ocorrer? Isso nos leva ao conceito de distribuição de probabilidades. Vamos começar com um cálculo simples: a probabilidade de todos sobreviverem até o tempo t, em nosso modelo estocástico apenas com mortes. Chamamos essa probabilidade de P(N(t)=N0). Como supomos que as probabilidades de morte são independentes entre indivíduos, seu valor é:
Probabilidade de todos sobreviverem P(N(t)=N0) = p(t)N0
Para tamanhos populacionais pequenos essa probabilidade pode ser alta como em nosso exemplo com N0=2 e p(t=1)=0,5:
P(N(t)=2) = 0,52 = 0,25
Já quando a população é grande, as chances de que todos sobrevivam são muito pequenas. O mesmo acontece para a probabilidade de todos morrerem, que é
P(N(t)=0) = (1−p(t))N0
É o raciocínio análogo a se perguntar qual a chance de ter apenas caras ou apenas coroas em um certo número de lançamentos de uma moeda. Todos os outros valores entre estes extremos são possíveis, e a cada um deles corresponde uma probabilidade, dada por:
P(N(t)\!=\!n) \ = \ \binom{N_0}{n} \ p(t)^n(1-p(t))^{(N_0-n)}
Esta é a distribuição binomial de probabilidades. Dado um certo número inicial de indivíduos N_0 com probabilidades iguais e independentes de morrer após um tempo t, essa distribuição dá a probabilidade de n indivíduos sobreviverem. De uma maneira mais geral, a binomial dá a probabilidade de n sucessos em N_0 tentativas, dada uma probabilidade constante de sucesso por tentativas.
A distribuição binomial
Para prosseguir você deve ter o ambiente R com os pacotes Rcmdr e Ecovirtual instalados e carregados. Se você não tem e não sabe como ter, consulte a página de Instalação.
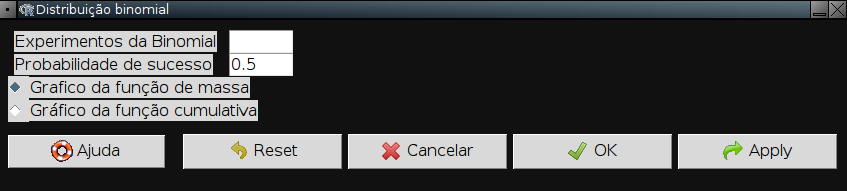
Vamos nos familiarizar com a ideia de distribuições de probabilidades, calculando valores da distribuição binomial. No menu do R Commander clique em Distribuições → Distribuições discretas → Distribuição binomial → Gráfico da distribuição binomial. Uma janela como esta vai se abrir:
com as opções:
| Opção | O que faz |
|---|---|
Experimentos da binomial | número de tentativas, no caso N_0 |
Probabilidade de sucesso | probabilidade de sucesso a cada tentativa, no caso probabilidade de cada indivíduo sobreviver |
Gráfico de função de massa / gráfico de função cumulativa | fazer gráfico de probabilidades por valor ou probabilidades acumuladas até este valor? |
Faça o gráfico de nosso exemplo:
- Na opção
Experimentos da binomialescreva 2 - Na opção
Probabilidade de sucesso: escreva 0.5 - Deixe marcada a opção
Gráfico de função de massa - Clique em
Apply
Você verá uma janela com o gráfico com o número de sucessos (no caso sobreviventes), que vai de zero a N_0, e suas probabilidades, de acordo com a distribuição binomial.
Arrume as janelas de maneira que a janela do gráfico e a das opções estejam lado a lado. Agora você pode avaliar o efeito de mudar os dois parâmetros da binomial: número de tentativas e a probabilidade de sucesso. Experimente alguns valores e proponha regras gerais sobre seus efeitos, clicando em Apply a cada tentativa. O gráfico irá se atualizar. Sugestões:
- Mantenha o número de tentativas em 10 e faça a probabilidade de sucesso ir de 0 a 1 a intervalos de 0,2
- Mantenha a probabilidade de sucesso em 0,5 e aumente o número de tentativas em 2, 5, 10, 100 , 1000.
Pergunta
Para uma população sob dinâmica estocástica apenas de mortes com taxa de mortalidade \mu=0,693 e tamanho inicial N_0=10:
- Calcule as probabilidades de sobrevivência para t=1, t=2 e t=3
- Faça os gráficos das distribuições de probabilidades dos tamanhos populacionais nestes 3 tempos
Simulação no computador
Até agora vimos algumas propriedades teóricas da dinâmica populacionais com estocasticidade demográfica:
- Há mais de um tamanho populacional possível a cada tempo;
- Quando há apenas mortes, a probabilidade dos tamanhos populacionais a cada tempo segue uma distribuição binomial;
- A média dos tamanhos populacionais a cada tempo corresponde ao valor previsto pelo modelo sem estocasticidade (determinístico).
Vamos agora testar na prática essas propriedades, e descobrir mais algumas, simulando populações com a dinâmica estocástica de mortes.
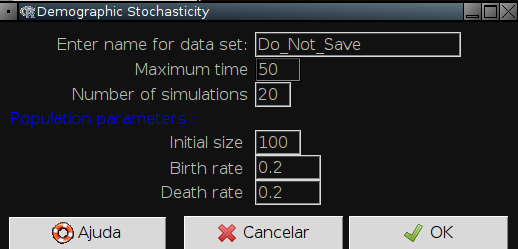
No menu do EcoVirtual clique em Ecovirtual → One Population → Demographic Stochasticity. Uma janela de diálogo como esta vai se abrir:
As opções controlam simulações de populações sob estocasticidade demográfica em tempo contínuo:
| Opção | O que faz |
|---|---|
Enter name for last simulation data set | nome para salvar os resultados da simulação em um objeto no R |
Maximum time | tempo máximo da simulação na escala de tempo das taxas |
Number of simulations | número de populações a simular |
Initial size | tamanho inicial das populações |
birth rate | taxa instantânea de nascimentos |
death rate | taxa instantânea de mortes |
Vamos simular dez populações de nosso primeiro exemplo, até o tempo 5. Para isso mude as opções de simulação para:
Maximum time: 5Number of simulations: 10Initial size: 2birth rate: 0death rate: 0.693
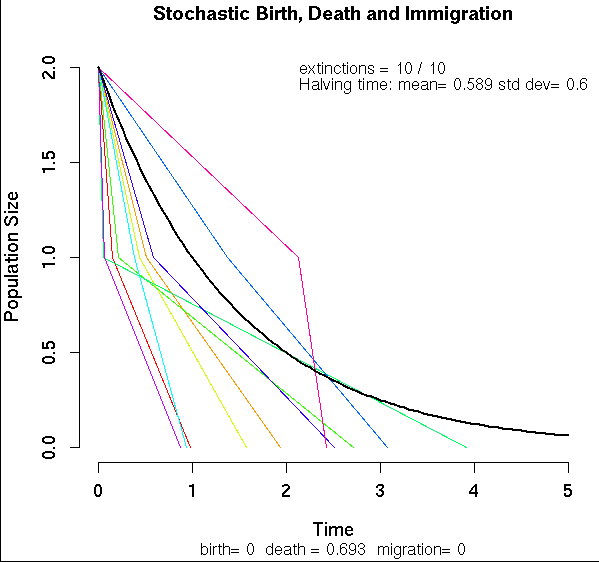
e clique em OK. Você deve ver um gráfico parecido com este:
As linhas coloridas são as trajetórias das dez populações, e a linha preta a trajetória esperada. No canto superior direito do gráfico está a média e o desvio-padrão do tempo que as populações levaram para diminuir pela metade (meia-vida da população).
Meia-vida da população
A meia-vida esperada em nossa simulação é de um ano, mas note como algumas populações demoraram bem mais do que outras para cair de dois para um indivíduo, ou para se extinguir. Vamos verificar se ainda assim o tempo médio para a população cair para metade corresponde ao valor teórico.
Testamos isso simulando muitas populações de tamanho inicial N_0=20 e calculando a média dos tempos que levaram para passar para N=10. Ajuste as opções de simulação para
Maximum time: 3Number of simulations: 1000Initial size: 20birth rate: 0death rate: 0.693
O gráfico vai ficar bem cheio de linhas, mas o que nos interessa é o valor em Halving time. A média está próxima do valor teórico? Agora aumente o tamanho inicial da população para 80, mantendo os outros parâmetros.
Perguntas
- Qual foi o efeito do tamanho populacional inicial sobre a média e a variação da meia-vida das populações?
- Qual a explicação para o resultado que você encontrou?
Distribuição dos tamanhos populacionais
Vamos inspecionar a distribuição dos tamanhos populacionais até o tempo t=2. Para isso temos que guardar os resultados em um objeto do R. Execute as simulações com os valores:
Enter name for last simulation data set: sim1Maximum time: 2Number of simulations: 1000Initial size: 20birth rate: 0death rate: 0.693
Clique em OK, e os resultados estão gravados em uma lista de 1000 tabelas no R, que chamamos sim1. Cada tabela tem os tempos em que a população perdeu um indivíduo e o tamanho da população a partir daquele momento, até o tempo máximo estipulado nas opções.
Para ver a primeira tabela, saia da janela da simulação clicando em Cancelar, e copie o comando abaixo na janela Script do Rcmdr
sim1[[1]]
e agora clique em Submeter.
A tabela será exibida na janela Output. Inspencione outras tabelas: execute de novo o comando, mudando o índice numérico que está entre os colchetes duplos, para qualquer valor entre um e mil.
Veja que os tamanhos das populações ao final da simulações (t=2) variam. Sabemos que os valores possíveis vão de N_0 (no caso 20) até zero. A distribuição probabilidade esperada para esses valores é a de uma binomial com N_0=20 tentativas e probabilidade de sucesso de p(t)=e^{-0,693 \times 2}=0,25. Faça o gráfico da distribuição com esses parâmetros usando o menu Distribuições do Rcmdr, como explicamos na seção sobre distribuições de probabilidades, acima.
Agora vamos comparar esse gráfico da distribuição teórica com os resultados das simulações. Faça um gráfico da proporção das simulações que terminou com cada tamanho executando os seguintes comandos:
## tamanhos finais de cada populacao sim1.Nt <- sapply(sim1, function(x)x[nrow(x),2]) ## Tabela de frequencia dos tamanhos populacionais sim1.tab <- table(factor(sim1.Nt, levels=0:20)) ## abre uma nova janela grafica x11() ## Grafico com as proporcoes esperadas de cada tamanho populacional plot(sim1.tab/1000, xlab="N(t=2)", ylab="Proporcao das populacoes", lwd=5)
Compare os dois gráficos. Há uma boa correspondência? Se quiser sobrepor os valores da binomial no gráfico das simulações copie e execute estes comandos:
## probabilidades esperadas pela binomial (sim1.esp <- dbinom(0:20, size=20 ,prob=.25)) lines(0:20,sim1.esp, col="blue", type="b")
Tamanho médio da população
Já guardamos o tamanho das mil populações simuladas em um objeto no R. Para obter a médias desses tamanhos copie e execute o comando
mean(sim1.Nt)
Pergunta
Esta média é compatível com o valor esperado?
Nascimentos e mortes
O que esperar de uma população com nascimentos e mortes estocásticos? O modelo resultante é uma extensão do anterior, com o acréscimo de que a probabilidade de aumento na população não é nula. Vamos usar o Ecovirtual para investigar o que muda.
Simulação em computador
Abra a janela Demographic Stochasticity e simule 200 populações com tamanho inicial 1 e com taxa de nascimento duas vezes maiores que a de morte. Execute as simulações com os valores:
Enter name for last simulation data set: sim2Maximum time: 20Number of simulations: 200Initial size: 1birth rate: 0.2death rate: 0.1
Os tamanhos populacionais agora oscilam em uma caminhada aleatória, devido à sucessão de nascimentos e mortes. Como a taxa de nascimentos é o dobro da de mortes, um nascimento é duas vezes mais provável do que uma morte, a qualquer instante. O senso comum diria então que as populações não correm risco de extinção. Será?
Tamanho populacional médio
De forma similar ao modelo anterior, o tamanho populacional esperado é
E[N(t)]=N_0e^{rt}
onde r é a taxa instantânea de crescimento, que é a diferença entre a taxa de nascimentos e de mortes.
Novamente guardamos os resultados em um objeto do R, do qual podemos calcular os tamanhos populacionais médios. Para isso copie e execute os comandos abaixo
sim2.Nt <- sapply(sim2, function(x)x[nrow(x),2]) mean(sim2.Nt)
Pergunta
Verifique se a média dos tamanhos populacionais das simulações é compatível com a média teórica.
Distribuição dos tamanhos populacionais
Mas já sabemos que a média não conta toda a estória. Como em qualquer modelo com estocasticidade, agora não temos mais um único valor possível para o tamanho populacional a cada tempo, e sim um conjunto de valores possíveis e suas respectivas probabilidades. Faça um histograma dos tamanhos populacionais no tempo final da simulação com o código
sim2.tab <- table(factor(sim2.Nt,
levels=0:max(sim2.Nt)))/length(sim2.Nt)
plot(sim2.tab, xlab="N(tmax)", ylab="Proporcao das populacoes", lwd=5)
No processo de mortes estocásticas vimos que as probabilidades de cada tamanho populacional a cada tempo seguem a distribuição binomial. Para um processo de nascimentos e mortes, as probabilidades seguem uma outra distribuição, chamada binomial negativa.
O que mais nos interessa aqui é que há uma probabilidade de um tamanho populacional zero, ou seja, de extinção das populações. Em nossas simulações, este N(t)=0 foi o valor mais frequente, o que é fácil de entender: como o tamanho inicial é de um indivíduo, há uma chance de um em dois de uma morte antes do primeiro nascimento, o que extingue a população.
Perguntas
- Para uma dinâmica estocástica com taxa de nascimentos maior que de mortes, qual é o efeito sobre a probabilidade de extinção de:
- Tempo de simulação?
- Tamanho inicial da população?
- Razão entre as taxas?
Utilize o EcoVirtual
- anote a cada simulação a proporção de populações extintas;
- faça um gráfico da probabilidade de extinção e as variáveis (tempo, tamanho e razão entre taxas);
- Compare suas conclusões com as obtidas se nascimentos e mortes se equivalem, como no roteiro de caminhada aleatória.
Para saber mais
- Renshaw, E. (1991). Modelling biological populations in space and time Cambridge University Press. Este roteiro segue a lógica do segundo capítulo desse livro, que é uma ótima introdução a modelos estocásticos de nascimentos e mortes.
- Akçakaya H.R., Burgman M.A & Ginzburg, L.V. (1999). Applied population ecology - Principles and computer exercises using RAMAS EcoLab. Outro livro muito didático, com exercícios em computador com o programa proprietário RAMAS ecolab. O capítulo 2 é uma excelente introdução às fontes de estocasticidade em dinâmicas populacionais.
- Tutoriais em R sobre distribuições de probablilidades discretas. Da disciplina Modelagem Estatística para Ecologia e Recursos Naturais, dos Programas de Pós-Graduação em Ecologia e em Recursos Florestais da USP. Incluem tutoriais sobre a distribuição binomial e binomial negativa.