Tabela de conteúdos
Padrões de gradientes em comunidades - simulação em R
Vamos construir uma comunidade virtual de plantas. Para isso vamos nos basear na distribuição de indivíduos em um gradiente ambiental. Partindo da premissa que as espécies tem uma distribuição normal de abundâncias ao longo do gradiente, podemos simular algo parecido com dados empíricos.
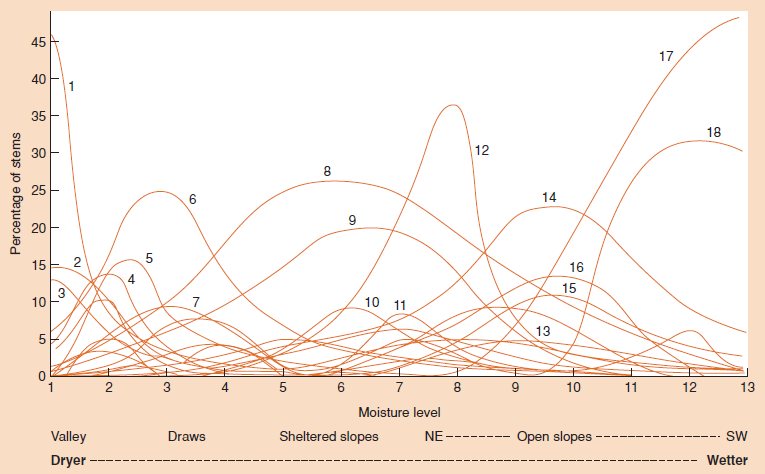
- Figura 16.6 do livro de Ecologia de Begon et al. (2006), mostrando a distribuição de espécies vegetais em um gradiente de umidade nas Montanhas Great Smoky, Tennessee. Dados retirados do trabalho clássico de Robert Whittaker. Cada curva representa a porcentagem de caules de uma espécie em relação ao total de caules em um local. Note como a distribuição normal pode ser uma boa aproximação das abundâncias das espécies ao longo de um gradiente.
A distribuição normal, ou Gausiana, tem dois parâmetros que correspondem à média e ao desvio-padrão. A partir desses parâmetros podemos construir curvas teóricas da proporção dos indivíduos de cada espécie ao longo do gradiente.
Gráfico do Gradiente
No R podemos facilmente criar uma comunidade com espécies que estejam distribuídas ao longo do gradiente. Copie e cole o função abaixo na linha de comando do R:
graf.com=function(medias, desvios, minimo, maximo, leg=TRUE)
{
dnorm.trunc=function(x, minimo=-Inf, maximo=Inf, media=0, desvio=1)
{
res=numeric(length(x))
x.prov=dnorm(x,mean=media, sd=desvio)
ampl.norm=pnorm(maximo,mean=media, sd=desvio)-pnorm(minimo,mean=media, sd=desvio)
x.prov/ampl.norm
}
nsp=length(medias)
cor=rainbow(nsp)
n.min=which.min(desvios)
curve(dnorm.trunc(x, medias[n.min], desvios[n.min], maximo=maximo, minimo=minimo),from=minimo, to=maximo, ylab="densidade da população", xlab="valor do gradiente", main="Distribuição no gradiente", col=cor[n.min])
seqsp=1:nsp
seqsp=seqsp[-n.min]
for (i in seqsp)
{
curve(dnorm.trunc(x, medias[i], desvios[i], maximo=maximo, minimo=minimo),from=minimo, to=maximo,add=TRUE, col=cor[i])
}
if(leg==TRUE)
{
n.medias=medias + (maximo-minimo) * 0.05
text(n.medias[n.min], dnorm.trunc(medias[n.min], medias[n.min], desvios[n.min],maximo=maximo,minimo=minimo), labels=paste("sp",n.min,sep="_"), col=cor[n.min], cex=.7)
text(n.medias[-n.min], dnorm.trunc(medias[-n.min], medias[-n.min], desvios[-n.min],maximo=maximo,minimo=minimo), labels=(paste("sp",seqsp,sep="_")), col=cor[-n.min], cex=.7)
}
}
Para criar o gráfico precisamos alimentar a função com as seguintes informações:
- os valores ótimos para cada espécie 1)
- as variâncias das espécies 2)
- o valor mínimo do gradiente
- o valor máximo do gradiente
Como usar a função??
Veja o exemplo abaixo:
graf.com(medias=c(2,3,4,5,6,7,8), desvios=c(1,1,1,1,1,1,1), minimo=0, maximo=10)
Não parece uma comunidade muito realística. No R é muito fácil criar sequências de números aleatórios a partir de alguma função conhecida. Siga passo a passo os seguintes comandos no R e veja o que eles estão gerando:
s1=seq(from=1.5, to=19.5, by=0.25) s1 med=sample(s1, size=10) med desv <-runif(10,0.5,2.5) desv
Tudo bem, eu explico!
- A primeira linha cria um objeto chamado s1 que é uma sequência de valores de 1,5 até 19,5 em intervalos de 0,25 3).
- A segunda linha só pede para mostrar o que o objeto s1 contém.
- 3a. linha: faz uma amostra de 10 valores dentre os que estão em s1 e guarda no objeto med
- 4a. linha: mostra os valores do objeto med
- 5a. linha: sorteia 10 valores, de um intervalo que vai de 0,5 até 2,5 e guarda esses valores no objeto desv
- 6a. linha: mostra os valores do objeto desv
Agora que criamos esses objetos, só precisamos executar a função que lê esses valores:
graf.com(medias=med, desvios=desv, minimo=0, maximo=20)
Dê uma olhada, como quem não quer nada, no gráfico do seu coleguinha ao lado. Por que o dele é mais bonito? Os gráficos não deveriam ser iguais já que ambos seguiram o mesmo roteiro, com o mesmo código? Rode os comandos abaixo, repetindo a segunda linha mais 3 vezes.
par(mfrow=c(2,2)) graf.com(medias=sample(2:19, size=10),desvios=sample(seq(from=0.5, to=2.5, by=0.1),10), minimo=1, maximo=20)
- A primeira linha do comando acima faz com que o dispositivo gráfico (uma janela gráfica) seja dividido em quatro partes, duas linhas e duas colunas. Para desligar, feche a janela gráfica que o padrão de um único gráfico por janela retorna.
- A segunda linha é a função que já conhecem para criar o gráfico da comunidade no gradiente. Para repetir essa linha de comando no R é só apertar a tecla ↑ que o R mostra a última linha de comando executado, se apertar novamente, a penúltima… Portanto, não precisa digitar ou copiar o comando do gráfico várias vezes, apenas aperte ⇑ e depois Enter
Você usou 4 vezes o mesmo comando para gerar comunidades virtuais. O que você observou?
Comunidade Discreta e Contínua
 Lembram da história, lá nos primórdios da ecologia, sobre dois pesquisadores com visões antagônicas de como as comunidades eram estruturadas? Um deles, Frederic Clements, tinha uma visão muito organizada das comunidades vegetais, com uma forte dependência mútua entre as espécies no sistema. Para Clements as comunidades vegetais funcionavam como um superorganismo que nasce, cresce e morre. Em contraste, o botânico Henry Gleason, na mesma época entendia as comunidades como um resultado da interação das espécies com o ambiente, combinada com acontecimentos ao acaso.
Legal, vamos brincar com essas ideias contrastantes em nosso gradiente ambiental virtual! Como reproduzir essas visões? Na primeira (mundo Clementsiano), as comunidades são discretas, ou seja, são compreendidas por um conjunto de espécies características que sempre ocorrem juntas. Já no mundo Gleisoniano as espécies têm limites de tolerância diferentes às condições ambientais e ocorrem independentemente das outras, ou seja, não há limites claros entre comunidades.
Lembram da história, lá nos primórdios da ecologia, sobre dois pesquisadores com visões antagônicas de como as comunidades eram estruturadas? Um deles, Frederic Clements, tinha uma visão muito organizada das comunidades vegetais, com uma forte dependência mútua entre as espécies no sistema. Para Clements as comunidades vegetais funcionavam como um superorganismo que nasce, cresce e morre. Em contraste, o botânico Henry Gleason, na mesma época entendia as comunidades como um resultado da interação das espécies com o ambiente, combinada com acontecimentos ao acaso.
Legal, vamos brincar com essas ideias contrastantes em nosso gradiente ambiental virtual! Como reproduzir essas visões? Na primeira (mundo Clementsiano), as comunidades são discretas, ou seja, são compreendidas por um conjunto de espécies características que sempre ocorrem juntas. Já no mundo Gleisoniano as espécies têm limites de tolerância diferentes às condições ambientais e ocorrem independentemente das outras, ou seja, não há limites claros entre comunidades.
Primeiro vamos montar uma comunidade contínua com 40 espécies em um gradiente de 0 a 150:
- sorteamos 40 valores de uma sequência de valores inteiros de 10 a 150, para representar o ótimo da espécie no gradiente
- sorteamos 40 valores de uma sequência que começa em 4 e vai até 10, a cada 0.5, para definir os desvios de cada espécie
- fazemos o gráfico da nossa comunidade virtual usando nossa função graf.com.
com.cont=sample(10:150, 40) desv=sample(seq(from=4, to=10, by=0.5),40, replace=TRUE) graf.com(medias=com.cont, desvios=desv, minimo=0, maximo=150)
Gerar comunidades discretas ao longo do gradiente é um pouco mais complicado. Nossas espécies devem formar grupos, ou associações, ao longo do gradiente. Vamos formar quatro grupos centrados nos valores: 30, 60, 90 e 120 do nosso gradiente. Para cada grupo sorteamos 10 espécies com algum desvio em torno do valor central. Para isso, vamos seguir esses passos:
- sorteamos 10 valores de uma distribuição normal com média 30 e desvio 5, para representar nossas primeiras 10 espécies
- repetimos o passo um para as médias de 60, 90 e 120
- usamos os mesmos valores de desvios da comunidade contínua (objeto desv criado acima) para as espécies
- construímos o gráfico das espécies no gradiente com esses valores, usando a função graf.com.
com1=rnorm(10, mean=30, sd=5) com2=rnorm(10, mean=60, sd=5) com3=rnorm(10, mean=90, sd=5) com4=rnorm(10, mean=120, sd=5) com.disc=c(com1,com2,com3,com4) graf.com(medias=com.disc, desvios=desv, minimo=0, maximo=150)
Vocês sentiram uma sensação de realização celestial? Agora temos poderes divinos… podemos criar nosso próprio mundo! Nada pode nos deter!!
Amostrando a Comunidade Virtual
Vamos retornar à nossa condição humana e seguir com um processo de amostragem da nossa comunidade. Vamos imaginar que esse gradiente existe e que as comunidades são exatamente essas que criamos, mas que não temos nenhuma informação prévia dos sistemas. Como somos humanos e queremos entender como as comunidades se estruturam, podemos nos fazer algumas perguntas, por exemplo:
- A comunidade responde ao gradiente ambiental?
- Se sim, essa resposta se dá por uma substituição gradual das espécies ao longo do gradiente ou por formação de subgrupos discretos de espécies em cada região do gradiente?
Para responder a essas perguntas, temos que ir ao sistema e conhecê-lo. Entretanto, não temos muito dinheiro nem tempo para estudar todas as espécies e todos os indivíduos que ocorrem ao longo de todo o gradiente, por isso tomamos a decisão de fazer uma amostragem. Como trata-se de um gradiente, podemos tomar a decisão de fazer essa amostra de forma sistemática em detrimento de uma completamente aleatória 4). Para isso vamos usar duas funções de amostragem abaixo amostra.com e prob.ssp. Copie e cole os códigos abaixo no R:
amostra.com=function(medias, desvios, amostra, n.ind=100, minimo=0,
maximo=150)
{
pnorm.trunc=function(x,minimo=-Inf, maximo=Inf, media=0, desvio=1)
{
denom <- pnorm(maximo, mean=media, sd=desvio) - pnorm(minimo, mean=media, sd=desvio)
qtmp <- pnorm(x, mean=media, sd=desvio) - pnorm(minimo, mean=media, sd=desvio)
qtmp/denom
}
nsp=length(medias)
namostra=length(amostra)
resulta=prob.resulta=matrix(0, nrow=nsp, ncol=namostra)
sp.name=paste("sp", 1:nsp, sep="_")
rownames(resulta)<-sp.name
colnames(resulta)=paste("plot", 1:namostra, sep="_")
for(k in 1:namostra)
{
for(i in 1:nsp)
{
prob.resulta[i,k]= pnorm.trunc(amostra[k]+1,minimo=minimo, maximo=maximo,media=medias[i], desvio=desvios[i])- pnorm.trunc(amostra[k],minimo=minimo, maximo=maximo,media=medias[i], desvio=desvios[i] )
}
s1=sample(sp.name, size=n.ind, prob=prob.resulta[,k], replace=TRUE)
conta.s1=table(s1)
pos.sp=match(names(conta.s1),sp.name)
resulta[,k][pos.sp]<-conta.s1
}
return(resulta)
}
Agora, vamos testar para ver se funciona. Lembre-se que já criamos os objetos que representam as medias e os desvios relacionados a cada uma das nossas comunidades. Para completar, temos que criar valores que representarão nossa amostra de cada comunidade. Entenda os passos:
- criar uma sequencia de 14 valores iniciando no 10 e terminando no 140 a cada 10. Esses valores representam os pontos do gradiente em que nossa amostra será realizada.
- amostrar a comunidade discreta a partir dos valores que usamos para criar os gráficos anteriores
- fazer o mesmo para a comunidade contínua
O código é o seguinte:
amost=seq(10,140, by=10) amost amost.disc<-amostra.com(medias=com.disc, desvios=desv, amostra=amost) head(amost.disc) amost.cont<-amostra.com(medias=com.cont, desvios=desv, amostra=amost) head(amost.cont)
Comparando a amostra com as comunidades criadas virtualmente
Até agora criamos nossas comunidades virtuais e fizemos uma amostra dela ao longo de um gradiente ambiental. Será que a amostra (composta pelos 14 pontos de amostragem) é fiel ao padrão expresso pela espécie no gradiente?5) Vamos colocar os valores lado a lado em um gráfico para investigar.
par(mfrow=c(2,2)) graf.com(medias=com.disc, desvios=desv, minimo=0, maximo=140) matplot(amost,t(amost.disc), type="l", lty=2, col=rainbow(dim(amost.disc)[1]), main="Amostra",xlab='valor do gradiente',ylab='indivíduos por parcela' ) graf.com(medias=com.cont, desvios=desv, minimo=0, maximo=140) matplot(amost,t(amost.cont), type="l", lty=2, col=rainbow(dim(amost.cont)[1]), main="Amostra",xlab='valor do gradiente',ylab='indivíduos por parcela' ) par(mfrow=c(1,1))
Agora temos uma amostra da comunidade discreta amost.disc, na qual as espécies ocorrem juntas em determinados pontos do gradiente e uma amostra da comunidade contínua amost.cont, na qual as espécies apresentam seus ótimos aleatoriamente dispostos no gradiente. Podemos então usar métodos analíticos de descrição de comunidades usuais em ecologia para verificar se com essas amostras conseguimos identificar os padrões das comunidades virtuais que criamos. Podemos até entender melhor as limitações e utilidades dos métodos, definindo a sensibilidade dos métodos para situações que esperamos encontrar no campo. Para isso vamos fazer as duas outras atividades propostas para esse módulo.
Um exercício interessante para você fazer em um outro momento (aquela hora que você está sem fazer nada em casa e fica procurando algo interessante na internet, sabe?) é montar comunidades discretas e contínuas com seus próprios parâmetros (número de espécies, tamanho do gradiente, amostra etc…). Tente rever como foram criadas as comunidade contínua e discreta do nosso roteiro e refaça os passos para criar as suas com novos parâmetros.
Para saber mais
Ainda no mundo dos mortais
Depois de “brincar de Deus” e criar seu gradiente ambiental, vamos continuar na pele do ecólogo que vai analisar esse gradiente, tentando descobrir se há algum padrão.
Conheça as análises que ecólogos usam para descobrir padrões a partir das variações de abundâncias das espécies. Os roteiros abaixo aplicam essas análises nos dados que você criou neste exercício:
- Classificação por agrupamento, ou análise de cluster.
Decifre o código
Caso queira entender melhor as funções em R, veja a versão deste roteiro com comentários do autor:
R comunidades análise_padrão